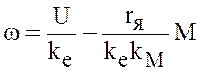Ответы на экзаменационные вопросы № 1-57 по дисциплине "Электропривод" (Электропривод, структурная схема, составные части. Расчет мощности и выбор типа двигателя), страница 6

                                            ,                                     (4)
где
        - напряжение якоря;
        - активное сопротивление якорной цепи;
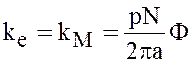        - конструктивный коэффициент;
       - число пар полюсов;
        - число активных проводников обмотки якоря;
       - число параллельных ветвей обмотки якоря;
       Ф – магнитный поток.

Тогда, применяя формулу (3) к (4), получим

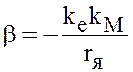                                              .                                               (5)

Перепишем уравнение механической характеристики ДПТ НВ (4) в виде

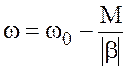                                               ,                                                 (6)

где
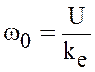                 - скорость холостого хода.

Из выражений (3) и (6) следует, что, чем больше жесткость  (по абсолютной величине), тем меньше скорость двигателя зависит от величины вращающего момента. С этой точки зрения большая величина  является полезным свойством для электропривода.

Анализ выражения (5) позволяет сделать следующие выводы.

·  Увеличение сопротивления цепи якоря (например, с помощью включения последовательно с обмоткой дополнительного сопротивления) приводит к уменьшению жесткости;

·  Величина напряжения якоря  не оказывает влияния на жесткость механической характеристики.

13. Вопрос

Жесткость механической характеристики АД в области точки номинального (паспортного) режима двигателя с координатами ,  может быть оценена следующим образом. Воспользуемся формулой Клосса, определяющей зависимость вращающего момента АД от величины скольжения

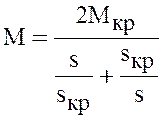                                                                               (7)

При малых значениях скольжения, что соответствует нормальной работе асинхронного двигателя, отношение  мало по сравнению с . Тогда, пренебрегая величиной  в знаменателе (7), получим выражение для вращающего момента в области номинальной скорости

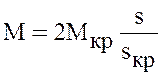                                      .                                    (8)

Затем, учитывая связь между скольжением и угловой скоростью двигателя

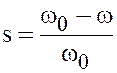                                    ,                                              (9)
приходим к приближенному выражению для механической характеристики АД в области номинальной скорости

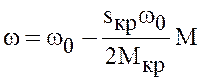                                   .                                  (10)

Выражение (10) есть уравнение наклонной прямой линии, проходящей через точку с координатами ,  (точку холостого хода) – рис. 19.

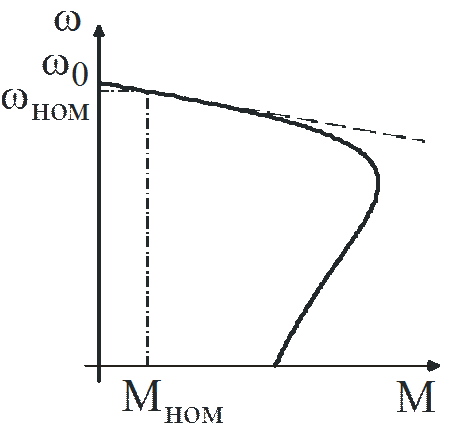
Рис. 19

Прямая линия (10) есть касательная к механической характеристике АД в точке холостого хода. Применяя (3) к выражению (10), получим жесткость механической характеристики АД

                                           .                                             (11)

Выражение (11) позволяет оценить жесткость в пределах рабочего участка механической характеристики.

Поскольку у АД величина критического момента 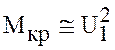, то, следовательно, и жесткость пропорциональна квадрату действующего значения напряжения на обмотках статора. С этой точки зрения асинхронный двигатель уступает двигателю постоянного тока независимого возбуждения, у которого жесткость не зависит от напряжения якоря.

Движение будет устойчивым при выполнении условия

                                                   ,                                           (12)

где

         и  - соответственно жесткость механических характеристик двигателя и исполнительного органа.

Нетрудно убедиться, что условие (12) для приведенного выше примера (рис. 17 )выполняется и движение является устойчивым.

14. Вопрос

Прямая линия (10) есть касательная к механической характеристике АД в точке холостого хода. Применяя (3) к выражению (10), получим жесткость механической характеристики АД

                                           .                                             (11)

Выражение (11) позволяет оценить жесткость в пределах рабочего участка механической характеристики.