Ответы на экзаменационные вопросы № 1-57 по дисциплине "Электропривод" (Электропривод, структурная схема, составные части. Расчет мощности и выбор типа двигателя), страница 2

4. Вопрос

Механика электропривода. Уравнение движения ЭП.

В механическом движении участвуют подвижная часть двигателя (ротор или якорь), элементы механической передачи и исполнительный орган рабочей машины. Движение любого элемента механической части ЭП описывается следующими дифференциальными уравнениями:

       при поступательном движении

;

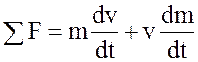       при вращательном движении

,

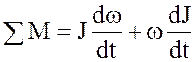где
                 и  - соответственно совокупность сил и моментов, действующих на элемент;
                m и J – масса и момент инерции элемента;
                v – скорость поступательного движения;
                 - угловая скорость.

В случае, если масса и момент инерции элементов в процессе движения не изменяются, уравнения движения упрощаются и принимают вид

,

,

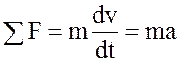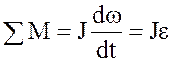где  - соответственно ускорение при поступательном и вращательном движении.

Если  или , то элемент движется с постоянной скоростью или находится в состоянии покоя. Такое движение называется установившемся.

При  или  элемент будет двигаться с ускорением, а при  или   - с замедлением.

5. Вопрос

Инерционные и упругие звенья.

Механическая часть электропривода, как правило, содержит промежуточные звенья между валом двигателя и исполнительным органом. Эти звенья разделяют на инерционные (роторы электродвигателей, редукторы, соединительные муфты и т.д.) и упругие – канаты, цепи, ремни и т.п. Такое разделение производят в зависимости от вида энергии, запасаемой в элементах.

Инерционные элементы запасают кинетическую энергию и характеризуются при поступательном движении – массой , кг; при вращательном движении - моментом инерции , кг*м².

Упругие элементы, деформация которых подчиняется закону Гука, запасают потенциальную энергию и характеризуются коэффициентом жесткости при растяжении или сжатии , Н/м, или коэффициентом жесткости при скручивании , Н*м/рад.

Коэффициент жесткости при растяжении (сжатии) – это коэффициент пропорциональности между линейной  деформацией  и возникающей в упругом элементе силой   (рис. 2)

.

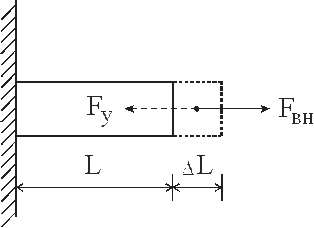
Рис. 2

Коэффициент жесткости при скручивании  - это коэффициент пропорциональности между угловой деформацией  и возникающем в упругом элементе моментом   (рис. 3)

.

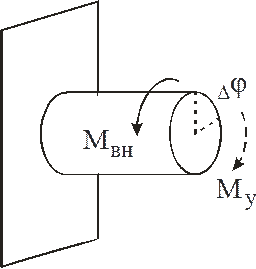
Рис. 3

6.Вопрос

Замена реальной кинематической схемы расчетной энергетически эквивалентной схемой. Приведение моментов инерции.

Элементы механической части привода механически связаны друг с другом и образуют единую кинематическую цепь от двигателя к исполнительному органу. Наличие промежуточных элементов вносит определенные искажения в процесс передачи движения от двигателя к исполнительному органу и требует соответствующего учета при анализе механического движения. С этой целью реальный механизм заменяют динамически эквивалентной, приведенной расчетной схемой, обладающей таким же энергетическим запасом, что и реальный механизм. Приведенная расчетная схема состоит из дискретных инерционных элементов, соединенных между собой упругими связями.

Под дискретным инерционным элементом понимают тело, обладающее свойством инерции, упругостью которого можно пренебречь.

Под упругой связью понимают упругое звено, массой которого можно пренебречь.

Приведение элементов реальной механической системы осуществляется к тому элементу кинематической цепи, движение которого подлежит рассмотрению. Обычно в качестве такого элемента приведения выбирают двигатель – источник механического движения.

В приведенной расчетной схеме все инерционные элементы осуществляют один вид движения – либо вращательное, либо поступательное.

В приведенных расчетных схемах вращательного движения все массы имеют общую геометрическую ось, нагрузки характеризуются крутящими моментами , Н*м; инерционные элементы – моментами инерции , кг*м² ; упругие элементы – коэффициентами жесткости при скручивании , Н*м/рад.