Ответы на экзаменационные вопросы № 1-57 по дисциплине "Электропривод" (Электропривод, структурная схема, составные части. Расчет мощности и выбор типа двигателя), страница 28

2) Возможностью оценки нагрузки двигателя. Если нагрев близок или равен нормативному, то нагрузка двигателя близка к номинальной и, следовательно, кпд и коэффициент мощности велики. Если нагрев существенно меньше нормативного, то это свидетельствует о недогрузке двигателя, низких кпд и коэффициенте мощности.

В тепловом отношении двигатель представляет собой неоднородный объект с изменяющимся (в зависимости от нагрузки) направлением тепловых потоков и неодинаковой температурой отдельных его частей. Так, на холостом ходу тепло передается от более нагретой стали к менее нагретым обмоткам, а при нагрузке – в обратном направлении. Как правило, большему нагреву подвержены те части обмотки, которые находятся во внутренних областях машины.

Точный расчет нагрева и охлаждения двигателей затруднен. При решении этой задачи принимают следующие упрощения:
          1) двигатель рассматривается как однородное тело, имеющее одинаковую температуру во всех точках;
          2) теплоотдача во внешнюю среду пропорциональна разности температур двигателя и окружающей среды;
          3) в процессе нагрева двигателя температура окружающей среды не изменяется.

Рассмотрим процесс нагрева двигателя за промежуток времени . Для этого составим уравнение теплового баланса (закон сохранения энергии применительно к тепловым процессам)
                                           .                                                   (4)

Физический смысл уравнения (4): количество энергии , выделевшейся в двигателе за промежуток времени , частично расходуется на повышение температуры двигателя  и частично отводится в окружающую среду .

Выразим составляющие (4) через электрические и тепловые параметры двигателя:

 - энергия, выделяющаяся в двигателе за счет потерь мощности ;
          ,
                    где  С – теплоемкость двигателя, Дж/^ОС – количество тепла, необходимое для повышения температуры двигателя на 1 ^ОС;
                             - температура двигателя;

,
                    где А – теплоотдача двигателя, Дж/(с^{. О}С) – количество тепла, отдаваемого двигателем за 1 с  в окружающую среду при разности температур двигателя и окружающей среды 1 ^ОС;
                           - температура окружающей среды.

Перепишем (4) с учетом принятых обозначений:
                            ,
или 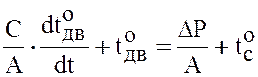                               .                                                     (5)

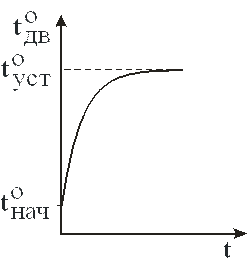
Следовательно, при принятых допущениях процесс нагрева двигателя описывается линейным дифференциальным уравнением первого порядка. Его решение имеет вид:

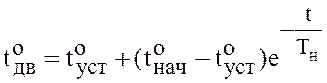                          ,                                      (6)
где 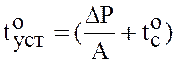       - установившаяся температура двигателя;
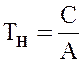        - постоянная времени нагрева двигателя.

График нагрева двигателя приведен на рис. 4.

Выражение (6) может применяться для моделирования процессов нагрева и охлаждения двигателя. При исследовании охлаждения следует учесть, что при неподвижном роторе условия вентиляции ухудшаются и теплоотдача двигателя уменьшается. Это приводит к увеличению постоянной времени охлаждения  по сравнению с постоянной нагрева 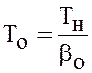                                                       .                                                (7)

Примерные значения коэффициента  для двигателей с различными системами охлаждения приведены в табл. 2.                                                Таблица 2

53. Вопрос

В соответствии с особенностями нагрева и охлаждения двигателей различают восемь режимов работы S1…S8, основными из которых являются:
          1) Продолжительный режим S1 – работа при постоянной нагрузке в течение такого времени, что температура всех частей машины достигает установившегося значения. График температуры и мощности потерь приведен на рис. 5.

Зависимость мощности потерь от времени , а также  называются нагрузочными диаграммами.