Ответы на экзаменационные вопросы № 1-57 по дисциплине "Электропривод" (Электропривод, структурная схема, составные части. Расчет мощности и выбор типа двигателя), страница 22

Приведем параметры неявнополюсной машины в относительных единицах:
                                               = ;
                                               = ;
                                               = .

Обозначим

                     - синхронное реактивное сопротивление обмотки статора.

Из сопоставления параметров машины следует, что , а величиной активного сопротивления обмотки статора  можно пренебречь. Тогда упрощенная схема обмотки статора принимает вид (рис.  ).

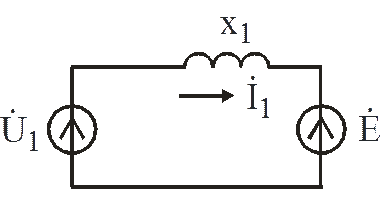
Составим для схемы рис.  второй закон Кирхгофа
                                                      .                                                  (1)

Векторная диаграмма, соответствующая уравнению (1), приведена на рис. .

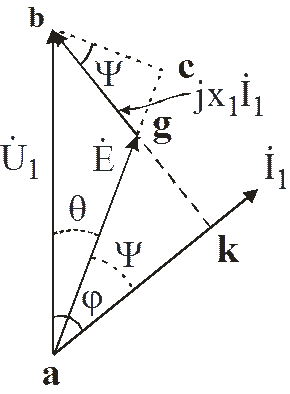
При работе машины в режиме двигателя вектор напряжения на статоре  опережает вектор ЭДС . Угол  между векторами  и  называют углом нагрузки. Он соответствует геометрическому углу между осью магнитного потока ротора  и осью результирующего магнитного потока , деленному на число пар полюсов ротора.

Пренебрегая незначительными потерями мощности на нагрев обмотки статора, потерями в стали и механическими потерями в машине, можно принять, что подводимая к СД мощность равна полезной мощности на валу
                                                           
или
                                                ,                                             (2)
где .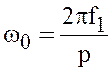

Отсюда вращающий момент
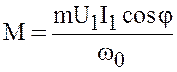                                              .                                                   (3)

Определим составляющие формулы (3).

Прямоугольные треугольники abc  и  gbc (рис. )  имеют общий катет bc. Определим его длину. Из треугольника abc:
                                             .                                                            (4)

Из треугольника gbc:
                                             .                                                         (5)

Сравнивая (4) и (5), получим
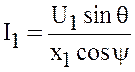                                             .                                                            (6)

Прямоугольные треугольники abk  и  agk (рис. )  имеют общий катет ak. Из треугольника abk:
                                              .                                                           (7)

Из треугольника agk:
                                              .                                                             (8)

Сравнивая (7) и (8), получим
                                          .                                                       (9)

Подставим (6) и (9) в выражение для вращающего момента (3)
                                     ,
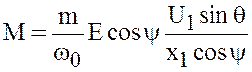или
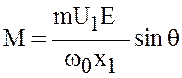                                            .                                                     (10)

При числе пар полюсов  в формулу (10) следует подставлять .

Зависимость вращающего момента синхронного двигателя от угла нагрузки называется угловой характеристикой – рис. .

С увеличением момента сопротивления на валу СД (от 0 до ) угол  возрастает. С увеличением угла нагрузки растет и вращающий момент двигателя, что удовлетворяет требованию устойчивой работы СД. При угле  вращающий момент достигает максимума
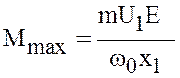                                               .                                                    (11)

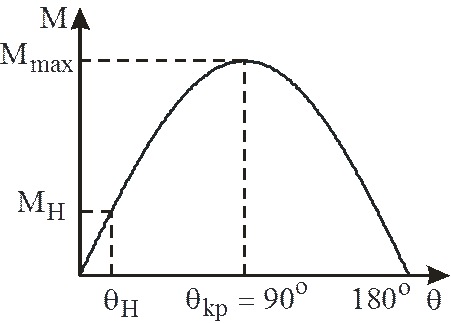
При  требование устойчивости нарушается, так как при увеличении нагрузки угол  продолжает расти, а момент, развиваемый двигателем, падает, в результате чего двигатель выпадает из синхронизма (останавливается).

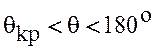Таким образом, левая часть угловой характеристики () является рабочей частью, а правая () является неустойчивой частью характеристики.

Номинальному моменту двигателя соответствует угол , что обеспечивает кратность максимального момента
                                                .

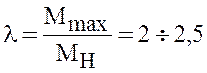Существуют синхронные двигатели с повышенной кратностью .