Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики

Точность и помехоустойчивость систем радиоавтоматики

3.1. Постановка задачи

Качество работы систем радиоавтоматики в установившемся режиме оценивается ошибками, создаваемыми регулярными и случайными воздействиями. Поскольку заранее вид воздействий неизвестен, качество работы оценивается показателями качества работы системы. При исследовании помехоустойчивости линейных систем используется принцип суперпозиции, и прохождение полезного воздействия  и случайной помехи  через систему рассматриваются раздельно (рис. 3.1). Соответственно ошибка на выходе системы  состоит из суммы динамической и флюктуационной составляющих ошибки.

Динамическая ошибка  создается при прохождении через систему полезного воздействия . Она может быть определена для регулярных или случайных воздействий. При расчете динамической ошибки для регулярных воздействий обычно задаются наибольшим значением параметра, влияющего на ошибку. Например, в случае авиационного дальномера с двумя интеграторами задаются максимальным значением ускорения, используемого при управлении самолетом.

Помехоустойчивость системы определяется величиной флюктуационной составляющей ошибки , создаваемой случайной помехой  и характеризуется дисперсией .

Если корреляция между динамической и флюктуационной ошибкой отсутствует,  квадрат суммарной ошибки  определяется выражением.

.

Системы РА в общем случае являются нелинейными устройствами. Однако при точном слежении и малых ошибках такие системы близки к линейным, и при проектировании используется теория линейных систем.

Исследование ошибок систем РА может выполняться частотными методами или во временной области.

          3.2. Точность при типовых регулярных воздействиях

Точность систем РА при типовых регулярных воздействиях характеризуется установившимся значением динамической ошибки.

            Полиномиальное входное воздействие имеет вид степенной функции времени :

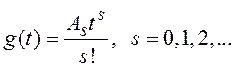,                                                     (3.1)

где  – порядок полинома.         

Функции (3.1) соответствует преобразование Лапласа

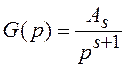.                                                     (3.2)

            Рассмотрим передаточную функцию разомкнутого контура системы, содержащей  интеграторов.

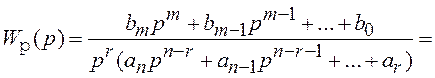
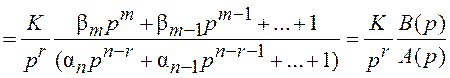,                              (3.3)

   где   ; ; ; , ; , .

            При отсутствии помехи  ошибка системы  определяется разностью входного  и выходного  сигналов. После преобразования Лапласа получим изображение ошибки  в виде

.

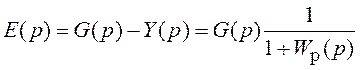            Используя свойство преобразования Лапласа о предельных значениях, найдем значение ошибки в установившемся режиме.

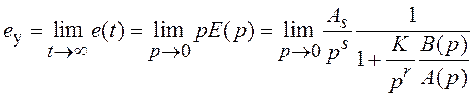 .                (3.4)

            Исследование выражения (3.4) показывает, что существуют следующие варианты

1.   значение ,

 2.  ,

3.      

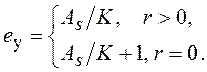
            Заметим, что при условии  система называется статической, а при  – астатической, причем  называется порядком астатизма.

Таблица 3.1

Зависимость величины установившейся ошибки  от порядка астатизма  для ряда типовых регулярных воздействий, показанных на рис. 3.2, представлена в табл. 3.1. В правом столбце приведен порядок формирующего

фильтра . Если порядок астатизма равен или превышает порядок формирующего фильтра, то установившаяся ошибка равна 0. В статической системе () при постоянном воздействии  существует ошибка, зависящая от коэффициента . В астатической системе первого порядка () при воздействии с постоянной скоростью  имеется скоростная ошибка , а при воздействии с постоянным ускорением  в системе второго порядка имеется ошибка .

3.3. Коэффициентный метод определения ошибок систем РА

            Рассмотрим произвольную функцию времени , имеющую ограниченное число производных. Этому требованию соответствует полиномиальная функция. Выполняя преобразование Лапласа, получим

.                                           (3.5)                                            

            Разложим  в ряд Тейлора в окрестности точки .

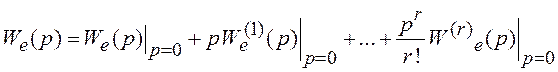.        (3.6)

            Введем определение коэффициента ошибок .

.

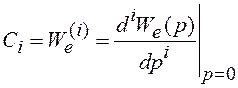            Тогда из (3.5) и (3.6) получим

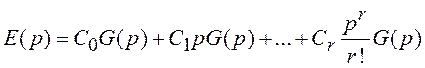.                              (3.7)

            Используя свойства преобразования Лапласа и выполняя предельный переход при , из (3.7) получим установившееся значение ошибки для .

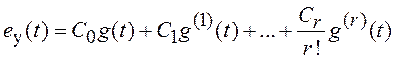,                          (3.8)

где .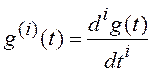

            С помощью выражения (3.8) можно вычислить установившееся значение ошибки как сумму составляющих, создаваемых входным воздействием  и его производными. Первое слагаемое определяется значением , второе – скоростью воздействия , третье – ускорением  и т.д.

 В астатических системах -го порядка коэффициенты ошибок  при , и в выражении (3.8) остаются только члены с индексами  и выше.