Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 5

Винеровский процесс формируется с помощью интегратора (рис. 3.9, а).

Дифференциальное уравнение этого процесса имеет вид  ,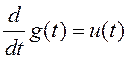

где  – белый гауссовский шум со спектральной плотностью . 

Для моделирования случайного изменения фазы генератора  используется формирующий фильтр (рис. 3.9, б), в котором скорость изменения фазы (частота ) является винеровским процессом.

Дифференциальные уравнения этого формирующего фильтра имеют вид.

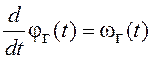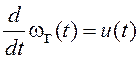; .                                                                      (3.25)

Уравнения (3.25) можно представить в векторной форме (3.12), если ввести обозначения ; ; .

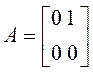Выполним переход к дискретному времени. Для составления разностного уравнения формирующего фильтра вида (3.19) используем представление вектора состояния  и определяем матрицу перехода  в виде ряда (1.    ). Используем два члена ряда, поскольку .

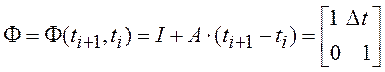, где  .          (3.26)                                                

            При расчете матрицы  используем выражение (3.20).

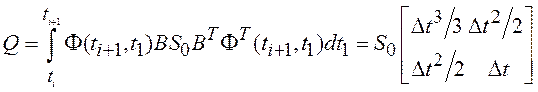.             (3.27)

            Из выражения (3.27) следует, что дискретный белый шум  состоит из двух составляющих . При этом дисперсия шума  имеет порядок , а шума  – порядок , и, следовательно, быстро убывает при уменьшении интервала дискретизации . Если подставить в  векторное выражение (3.19) значение  и  из (3.26), получим систему разностных уравнений.

; .            (3.28)

            Системе (3.28) соответствует структурная схема, показанная на рис. 3.9,в.

            Можно построить фильтр для формирования процесса, ускорение которого является винеровским процессом. Вектор состояния этого процесса имеет вид , а система дифференциальных уравнений фильтра содержит три уравнения.

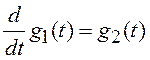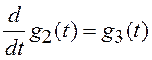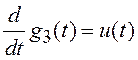; ; .                         (3.29)

Матрицы векторного дифференциального уравнения , .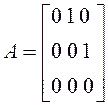

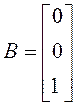            Можно показать, что матрицы векторного разностного уравнения для дискретного времени равны:

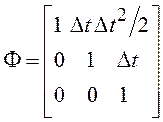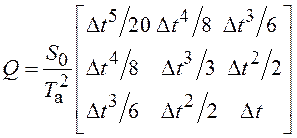, .                     (3.30)

Формирующий фильтр для получения экспоненциально-коррелированного процесса с постоянной времени  (рис. 3.10, а) строится на основе выражения (1.    ) и определяется дифференциальным уравнением

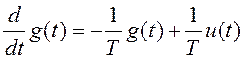.                                   (3.31)

            Разностное уравнение для этого процесса имеет вид

 ,                                                           (3.32)

 а переходная матрица определяется из решения линейного дифференциального уравнения (1..) 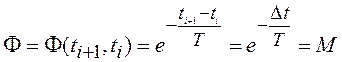. Вместо матрицы  в данном случае с помощью выражения (3.20) определяем дисперсию дискретного шума .

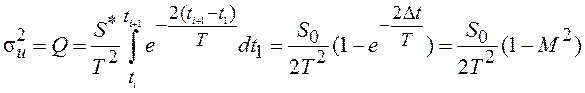.         (3.33)

Уравнению (3.32) соответствует структурная схема на рис. 3.10, в.

Процесс с экспоненциально-коррелированной скоростью используется для моделирования случайной ошибки счисления пройденного самолетом пути , вызванной ошибкой измерения скорости  (рис. 3.10, б). При использовании датчика воздушной скорости ошибка  создается из-за действия ветра, имеющего интервал корреляции скорости . Дифференциальные уравнения этого процесса имеют вид.

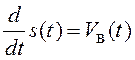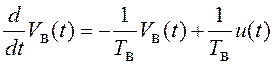;.                                              (3.34)

При преобразовании выражений (3.34) в векторную форму (3.12)  необходимо ввести ; ; .

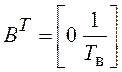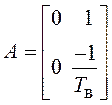При построении разностного уравнения в дискретном времени находим матрицу перехода с помощью выражения (1.37).

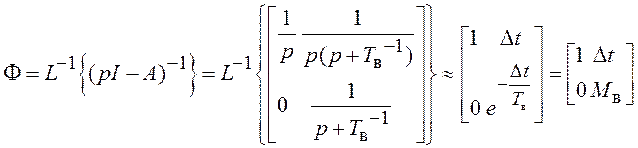.     (3.35)

При вычислении обратного преобразования Лапласа в выражении (3.35) было выполнено приближение .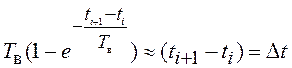

При расчете матрицы  используем выражение (3.20).

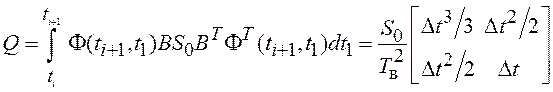.                 (3.36)          

Используя выражение (3.35), получим систему разностных уравнений.

;.                        (3.37)

            Уравнениям (3.37) соответствует структурная схема на рис. 3.10, г.

Для моделирования случайной составляющей пройденного самолетом пути  используется процесс с экспоненциально-коррелированным ускорением . При этом предполагается, что ускорение самолета имеет интервал корреляции   (десятки секунд). Вектор состояния формирующего фильтра содержит составляющие пути , скорости  и ускорения .

  Система дифференциальных уравнений фильтра имеет вид.