Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 7

,                             (3.49)

где –-мерный вектор;  – матрица размером ;  – матрица  размером .

Вычислим вектор ошибки фильтрации .

,

            Подставляя (3.48) и (3.49) определим значение вектора ошибки

.

            Выполнив усреднение, получим

.                                         (3.50)

            Потребуем, чтобы ошибка  не имела смещения при наличии условия . Тогда из выражения (3.50) следует, что  и уравнение (3.49) принимает вид

                        (3.51)                      

Уравнение (3.51) эквивалентно уравнению системы согласованной структуры (1.32), полученному для непрерывного времени. На рис. 3.13 показана структура дискретной системы, ошибка которой не имеет смещения при произвольном значении . Отметим, что в этой системе используются элементы формирующего фильтра  и .

Уравнение ошибки системы без смещения имеет вид:

.                                  (3.52)                       

            Найдем уравнение для дисперсионной матрицы ошибки фильтрации, используя выражение (3.52) для вектора .

.         (3.53)

            При выводе этого уравнения использовалось предположение об отсутствии корреляции между ошибкой  и шумами  и .

            Если определить матрицу ошибок экстраполяции с помощью выражения , то из (3.53) можно получить

.             (3.54)

            Решение дисперсионных уравнений (3.53) и (3.54) выполняется с помощью ЭВМ. При этом матрицы , , ,  и  могут быть функциями дискретного времени.

Пример 3.5. Для систем низкого порядка с постоянными матрицами можно получить стационарное значение дисперсионной матрицы ошибок  при условии  .

Для формирующего фильтра с одним дискретным интегратором, на вход которого поступает дискретный белый шум, уравнения (3.47) и (3.48) принимают вид

,

.

Уравнение системы с одним интегратором в соответствии с (3.49) имеет вид              .                                                          (3.55)

В рассматриваемом примере , , , .

Тогда из выражения (3.53) получим дисперсионное уравнение.

.

При   и .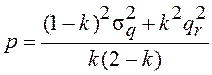

Значение  при . Такое значение  соответствует области устойчивости системы (3.55).

Устройства радиоавтоматики

          4.1. Введение

В современных радиотехнических системах широко используются следящие измерители дальности, угловых координат, частоты и фазы радиосигналов.

            Общая структура следящего измерителя состоит из дискриминатора,  сглаживающего фильтра и модулятора (рис. 4.1). Принятый радиосигнал , содержащий измеряемый параметр , поступает на вход дискриминатора, на второй вход которого подается напряжение с выхода модулятора, содержащее оценку параметра . Дискриминатор вырабатывает сигнал рассогласования , пропорциональный разности . Сигнал рассогласования поступает на сглаживающий фильтр, вырабатывающий выходной сигнал измерителя . Этот сигнал пропорционален оценке параметра и с помощью модулятора преобразуется в оценку .

При аналоговой реализации следящего измерителя дискриминатор вырабатывает сигнал рассогласования в виде напряжения, которое затем поступает в сглаживающее устройство. В радиолокационных измерителях угловых координат и дальности в качестве сглаживающих устройств находят применение электромеханические системы с двигателями, вращающими антенну или механический стрелочный индикатор.  В аналоговых системах автоматической подстройки частоты и фазы широко используются сглаживающие фильтры с операционными усилителями. В качестве модулятора используются управляемые генераторы – например, генератор с переменной частотой при слежении за частотой. В угломере со следящей антенной модуляцию принимаемого сигнала выполняет антенная система.