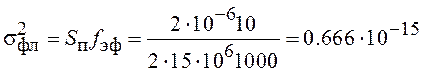Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 24

[].

[мкс] или в единицах расстояния  (1мкс – 300м) [м].

Пример 4.3. Выполним расчет дисперсии отсчета фазы сигнала, используемого в радионавигационной системе ГЛОНАСС. Отношение сигнал/помеха равно 30 дБ Гц. Из табл. 4.1 и выражения (4.41) вычислим дисперсию ошибки измерения фазы по одному элементарному символу  и из (4.40) спектральную плотность ошибки на нулевой частоте .

Зададимся эффективной полосой измерителя фазы Гц, и получим 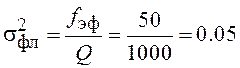 и 0.227.

Ошибка системы фазовой подстройки измеряется в радианах. Произведем расчет среднеквадратического значения ошибки слежения за фазой в единицах расстояния. Изменению фазы на  соответствует изменение расстояния на длину волны . В системе ГЛОНАСС частота сигнала МГц,   см и  см.

Точность фазовых измерений существенно превосходит точность измерений задержки кодированного сигнала из предыдущего примера. Однако для реализации этой точности необходимо решить сложную задачу устранения неоднозначности фазовых измерений.

4.11. Флюктуационные характеристики дискриминаторов

Дисперсия ошибки на выходе дискриминатора и, следовательно, спектральная плотность   в общем случае зависят от величины рассогласования e. Зависимость  называется флюктуационной характеристикой.

Исследуем флюктуационную характеристику дискриминатора на примере моноимпульсного угломера, принимающего флюктуирующий импульсный сигнал. Выполним расчет дисперсии ошибки единичного отсчета угловой координаты при приеме сигналов вида

 и

,

где  и  – напряжения суммы и разности полезного сигнала,  и   – широкополосные шумы, статистически независимые между собой.

            На выходе фазового детектора после умножения напряжений суммы и разности получается напряжение

                                    (4.42)

            Постоянная составляющая может содержаться лишь в первом слагаемом выражения (4.42), так как напряжения сигнала и шумов не коррелированны между собой.

            Таким образом, величина сигнала ошибки не зависит от уровня шума, и крутизна дискриминационной характеристики может быть определена из выражения (4.21).

Найдем спектральную плотность мощности случайных флюктуаций напряжения на выходе фазового детектора. Случайные флюктуации первого слагаемого в выражении (4.42) вызваны флюктуациями отраженного сигнала, во втором и третьем – биениями между сигналом и шумами и в последнем – детектированием шумов. Корреляция между сигналом и шумами, а также между шумами  и  отсутствует, поэтому спектральная плотность мощности напряжения  равна сумме спектральных плотностей отдельных составляющих.

При расчетах предполагаем, что огибающая случайных флюктуаций сигнала первого слагаемого изменяется во времени медленно и проходит через схему фиксации без искажений.

Используя (4.20) вычислим корреляционную функцию случайных флюктуаций, содержащихся в первом слагаемом. 

.                        (4.43)

            Далее воспользуемся известной формулой четвертого смешанного момента для нормальных случайных величин:

                                                   (4.44)

            Из (4.43) и (4.44) получим

,

где  –действующее значение напряжения сигнала на выходе УПЧ суммарного канала; – корреляционная функция флюктуаций сигнала; .

Примечание. При вычислении корреляционной функции принято во внимание то обстоятельство, что в произведении двух высокочастотных процессов часть энергии произведения приходится на высокочастотные составляющие двойной частоты, которые отфильтровываются при дальнейшей обработке. Если сигналы  и  имеют корреляционные функции вида  и , то корреляционная функция  произведения имеет вид 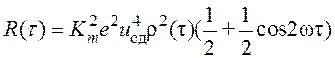, и слагаемое с двойной частотой отбрасывается.

            Интегрируя функцию корреляции  по  и разделив на квадрат крутизны дискриминационной характеристики , получим значение эквивалентной спектральной плотности на нулевой частоте, создаваемой флюктуациями сигнала.