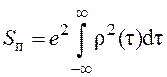Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 25

.                                                        (4.45)

Применяя формулу (4.44) ко второму, третьему и четвертому слагаемым в (4.42), получим суммарную дисперсию напряжения ошибки, создаваемой действием шумов.

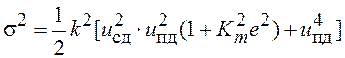,                                (4.46)

где  – действующее значение напряжения шумов на выходах УПЧ суммарного и  разностного каналов.

Случайные флюктуации, создаваемые шумами, не коррелированны в различных периодах сигнала. Поэтому при расчете спектральной плотности используем выражение (4.40). Разделив (4.46) на  и объединяя с (4.45), получим выражение для суммарной эквивалентной спектральной плотности угловых флюктуаций.

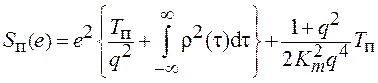            ,                                    (4.47)

где – отношение мощностей сигнала и помехи; .

            Первое слагаемое в выражении (4.47), зависящее от квадрата рассогласования , содержит составляющую биений сигнала и шума и составляющую амплитудных флюктуаций. Подобные выражения можно получить и при измерении задержки радиосигналов.

            Зависимость  от рассогласования по угловой координате  показана на рис. 4.32. В общем случае величина  зависит от ошибок слежения, и следящий измеритель действует как система с переменными параметрами. При использовании частотных методов анализа случайных ошибок следящих измерителей зависимость спектральной плотности от ошибок не учитывается, и спектральная плотность предполагается постоянной. При малой величине отношения сигнала и помехи возрастает вклад второго слагаемого в выражении (4.47), не зависящего от рассогласования, и   становится постоянной.

            В фазовых дискриминаторах спектральная плотность  не зависит от рассогласования [   ], однако в частотных дискриминаторах имеется существенная зависимость от частоты.

            Произведем расчет СПМ флюктуаций на выходе цифрового частотного детектора, использующего алгоритм (4.28). Полагаем, что сигналы  и  с частотой  имеют вид

, ,                                   (4.48)

где  – амплитуда сигнала;   и  – квадратурные составляющие узкополосного шума.

            Обозначив выходной сигнал частотного детектора , из выражений (4.28) и (4.48) получим среднее значение оценки частоты . При малых значениях частоты  можно получить . Таким образом, значение крутизны дискриминационной характеристики цифрового частотного детектора .

            Из выражений (4.28) и (4.48) получим далее флюктуационную составляющую напряжения на выходе частотного детектора.

.                       (4.49)

Затем из (4.49) определим средний квадрат флюктуационной ошибки

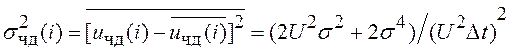,                           (4.50)

где  – дисперсия квадратурных составляющих шума.

            В цифровом частотном детекторе используются значения квадратурных составляющих в соседних интервалах времени  и . Поэтому отсчеты   в соседних интервалах времени коррелированны. Определим корреляцию между отсчетами  и .

.   (4.51)

            Из-за наличия корреляции в соседних отсчетах корреляционная функция случайной составляющей ошибки на выходе частотного детектора имеет вид, показанный на рис. 4.33. Наличие отрицательной корреляции повышает эффективность фильтрации. Спектральная плотность  равна

.   

В области нулевой частоты , и используя (4.50) и (4.51) получим

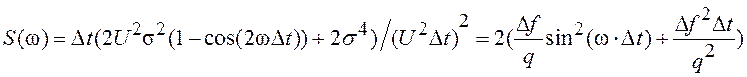,    (4.52)                                             

где  – отношение сигнал/помеха; ; ; ;  – спектральная плотность шума;  – полоса пропускания радиоканала.

          В выражении (4.52) первое слагаемое зависит от частоты (вблизи нулевой частоты зависимость параболическая), а второе не зависит. Зависимость спектральной плотности от рассогласования по частоте подобна рассмотренной выше зависимости спектральной плотности (рис. 4.32) для дискриминатора моноимпульсного угломера. При  наибольший вклад вносит первое слагаемое выражения (4.52), зависящее от  частоты. При уменьшении  возрастает роль второго слагаемого, не зависящего от частоты.