Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 2

            Пример 3.1. Определим коэффициенты ошибок статической системы с передаточными функциями разомкнутой системы  и ошибок 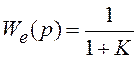, соответственно. Коэффициент 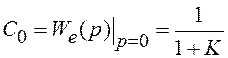. Тогда ошибка по положению 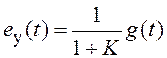. При постоянном  установившаяся ошибка постоянна (рис. 3.3 а), но при линейно изменяющемся  ошибка бесконечно растет с течением времени 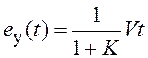 (рис. 3.3 б).

3.4. Описание случайных процессов

Случайные ошибки систем радиоавтоматики создаются за счет случайных помех в каналах распространения радиосигналов и случайных флюктуаций отслеживаемого параметра  (например, частоты и фазы задающих генераторов).

Случайные ошибки систем радиоавтоматики являются случайными функциями времени, и характеризуются вероятностными и корреляционными характеристиками. Вероятностная характеристика случайной величины  определяется плотностью распределения вероятностей  и ее моментами. В качестве примера можно привести нормальный (гауссовский) закон распределения.

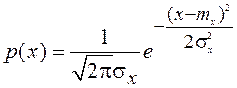,                                    (3.9)

где  – среднее значение; 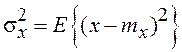 – дисперсия;  – среднеквадратическое отклонение.

            Среднее значение является  постоянной составляющей стационарного случайного процесса, а дисперсия – средней энергией отклонения .

            Широкое применение нормального закона объясняется тем, что при воздействии широкополосного шума с произвольным распределением на узкополосную линейную систему в силу центральной предельной теоремы Ляпунова на выходе системы формируется случайный процесс с нормальным законом распределения.

            В нелинейных системах закон распределения случайной величины может отличаться от нормального. Ошибки цифровой обработки часто имеют равномерное распределение. Например, ошибка дискретизации при аналого-цифровом преобразовании  имеет равномерное распределение          

в интервале значений (,), соответствующем величине младшего разряда АЦП  (рис. 3.4).

            В качестве корреляционной характеристики стационарного случайного процесса используются автокорреляционная функция (временная область) или спектральная плотность мощности (частотная область).

            Автокорреляционная функция (АКФ) процесса  с нулевым средним определяется выражением.

.

            Значение АКФ при  равно дисперсии случайного процесса .

 Для стационарного случайного процесса ,  и

можно получить спектральную плотность мощности :

,

где  – преобразование Фурье.

            При этом ,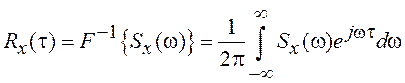

где  – обратное преобразование Фурье.

            Очевидно, что 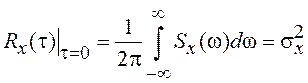.                                       (3.10)

Для векторного случайного процесса  можно определить среднее значение  и корреляционную матрицу  .

,

.

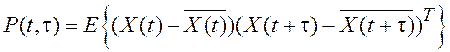Если нас интересуют только дисперсионные свойства векторного случайного процесса, то используют дисперсионную матрицу

 .

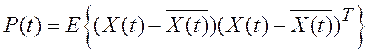 Для случайного процесса  с нулевым средним

 .

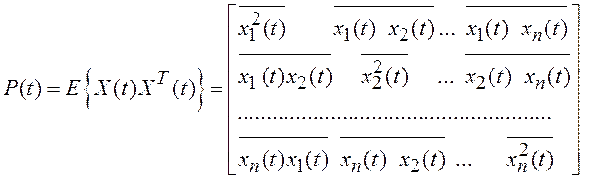Дисперсионная матрица  симметрична, то есть . На главной диагонали дисперсионной матрицы располагаются дисперсии компонент векторного случайного процесса  , остальные элементы отражают взаимную корреляцию компонент. По этой причине эту матрицу часто также называют корреляционной.

Для случайного вектора   с нормальным законом распределения плотность распределения вероятности  равна

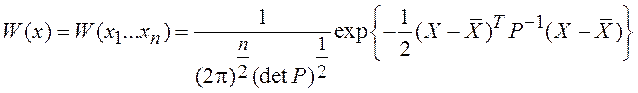.    (3.11)

В выражении (3.11) среднее  и дисперсионная матрица  полностью характеризуют вероятностные характеристики вектора .

3.5. Описание случайных процессов во временной области

Частотные методы и спектральные характеристики случайных процессов используются при исследовании систем с постоянными параметрами. Это ограничение можно снять, применяя временные методы для описания систем и процессов. Для моделирования случайного процесса  используем дифференциальное уравнение, подобное (1.9).

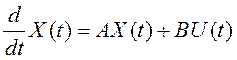,                                  (3.12)

где  – -мерный вектор;  – матрица размером ,  – матрица размером ,  – случайный -мерный вектор белого гауссовского шума с нулевым средним и диагональной корреляционной матрицей . Матрицы ,  и  могут быть функциями времени.