Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 3

В дифференциальном уравнении (3.12) содержатся составляющие вектора шума , имеющие бесконечную дисперсию. Подобный шум реально не существует, но такая модель шума позволяет существенно упростить математические вычисления.  Реальный случайный процесс можно приближенно заменить белым шумом, если интервал корреляции случайного процесса намного меньше постоянной времени исследуемой системы. Поэтому в инженерной практике широко используется представление случайного процесса вида (3.12).

Так как уравнение  (3.12) линейное, то процесс  имеет нормальное распределение, которое характеризуется средним значением  и дисперсионной матрицей .

 Усредняя  (3.12) , получим уравнение

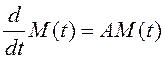, .                                   (3.13)

Отметим, что при нулевом начальном условии  значение .

Для определения дисперсионной матрицы  находим решение векторного дифференциального уравнения (3.12) в виде (1.28).

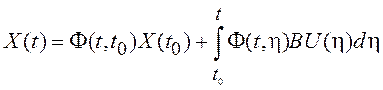.                   (3.14)

            Дисперсионная матрица случайного вектора  с нулевым средним определяется как

.                                           (3.15)

            Выполняя подстановку  из (3.14) в (3.15) и принимая во внимание отсутствие корреляции  и шума , получим в результате усреднения

.

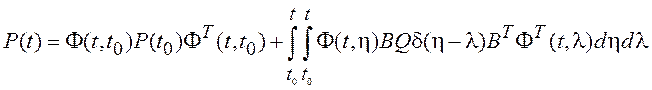Далее, используя фильтрующие свойства дельта-функции, вычислим интеграл по переменной .

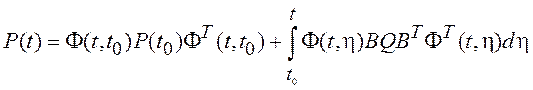.             (3.16)

Выражение (3.16) трудно вычислить, так как не всегда можно определить явное выражение для матричной экспоненты. Оказывается более удобным для вычислений дифференцировать это выражение и получить дифференциальное уравнение

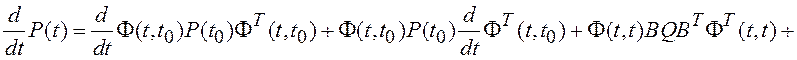
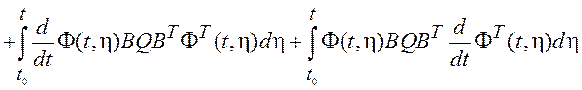.                   (3.17)

Подставив в (3.17) 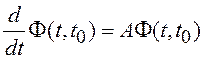 и  , можно затем сгруппировать первое и третье слагаемое, а так же второе и последнее. Тогда подставив (3.16) в (3.17), получим дисперсионное уравнение:

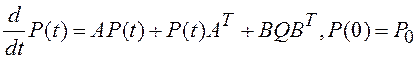.                               (3.18)

Это дифференциальное уравнение может быть решено с помощью ЭВМ.

Если процесс  стационарный, то при  матрица , , 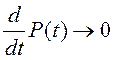и дифференциальное уравнение (3.19) превращается в алгебраическое уравнение.

При цифровой реализации устройств радиоавтоматики необходимо выполнить дискретизацию случайного процесса во времени, то есть заменить непрерывный процесс  последовательностью отсчетов , ,  и так далее (рис. 3.5). При дискретизации используем решение дифференциального уравнения (3.14). На первом интервале времени  находим .

.

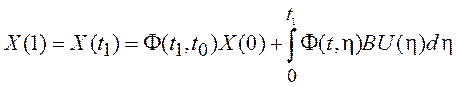Затем используем  в качестве начального условия для вычисления  на следующем интервале. Если матрица  не зависит от времени, то при постоянном интервале дискретизации  матрица , и на момент времени  получим

,                                                   (3.19)

где  – -мерный вектор; .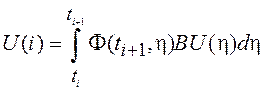

Шум  имеет нулевое среднее, и случайный вектор  также имеет нулевое среднее. Значения процесса  в соседних интервалах времени не коррелированны, так как при их вычислении производится интегрирование белого шума  на не перекрывающихся интервалах времени. Поэтому процесс   называется дискретным белым шумом.

Определим корреляционную матрицу дискретного белого шума .

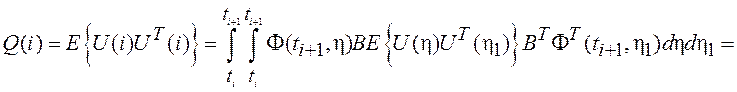
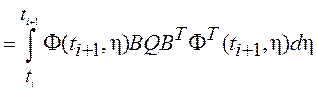.                                       (3.20)

Отметим, что случайные процессы  и  являются марковскими случайными процессами, обладающими следующим важным свойством. Для любых последовательных моментов времени  условная плотность вероятности процесса зависит только от состояния процесса в предыдущий момент времени

.

Это свойство марковских процессов существенно упрощает построение оптимальных алгоритмов фильтрации и управления.

3.6. Анализ помехоустойчивости систем РА в частотной области

Для анализа помехоустойчивости в частотной области используется спектральная плотность мощности помехи на входе  и частотная характеристика замкнутой системы .

Спектральная плотность мощности флюктуаций на выходе системы равна

.

В радиотехнических системах помехи часто имеют широкополосный спектр, и в пределах частотной характеристики системы спектральная плотность  постоянна (рис. 3.6).   Тогда  , и

.                                          (3.21)

Используем выражения (3.10) и (3.21) для расчета дисперсии флюктуационной ошибки.

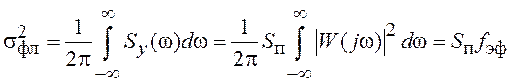,                  (3.22)