Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 4

где 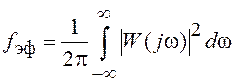 – эффективная (шумовая) полоса системы.

В выражении (3.23) интегрирование выполняется в пределах (), эффективная полоса  вычисляется в этих же пределах, и  является двусторонней спектральной плотностью. Иногда используют понятие односторонней спектральной плотности, которая вдвое больше двусторонней . Однако использование пределов () позволяет упростить вычисление интегралов.

Табл. 3.2

Если комплексная частотная характеристика замкнутой системы  представлена в виде дробно-рациональной функции, интеграл в (3.22) приводится к табличному интегралу вида

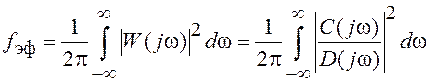,                               (3.23)

где ;.

Приведем значения интеграла (3.23)   для :

; ; .

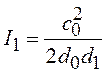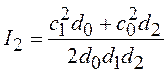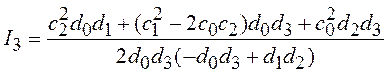Выражение (3.23) позволяет для ряда наиболее распространенных систем использовать известные результаты при определении  (табл. 3.2).

Пример 3.2. Рассмотрим систему с передаточной функцией 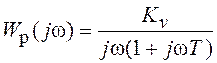. В этой системе, как видно из табл. 3.2, эффективная полоса пропускания не зависит от постоянной времени . Чтобы объяснить это явление, построим ЛАЧХ  и квадрат АЧХ  при различных постоянных времени.

Увеличение постоянной времени  снижает частоту среза  (рис. 3.7 а) и уменьшает полосу пропускания системы. Однако увеличение постоянной времени  снижает запас устойчивости, так как частота среза  смещается на участок ЛАЧХ с крутизной –12дБ/окт. В результате на частотной характеристике замкнутой системы появляется выброс (резонансный пик) в районе , и площадь функции  не изменяется (рис. 3.7 б).

3.7. Точность при случайных входных воздействиях

            Расчет точности при действии случайных воздействий на систему радиоавтоматики основан на предположении, что полезное воздействие  формируется из белого шума  с помощью формирующего фильтра с функцией передачи  (рис. 3.8). Ошибка системы  в данном случае является случайным процессом. Спектральная плотность мощности ошибки системы равна

,

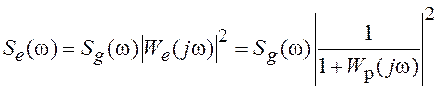где 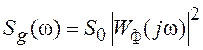;  – спектральная плотность белого шума .

            Дисперсия ошибки системы при случайном полезном воздействии равна

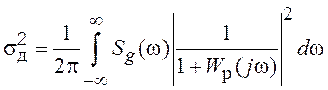.                                (3.24)

Интеграл в (3.24) вычисляется указанным в разд. 3.6 способом.

Рассмотрим наиболее часто используемые модели случайных воздействий, формируемых с помощью фильтрации белого шума .

1)  При интегрировании белого шума формируется винеровский процесс,

спектральная плотность мощности которого равна:

.

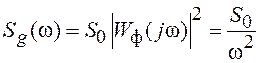Дисперсия такого процесса бесконечно растет с течением времени:

.

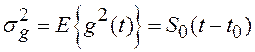 Винеровский процесс является нестационарным, и вычислить его дисперсию с помощью частотных методов нельзя.

 Пример 3.3. Выполним расчет дисперсии ошибки системы с функцией передачи 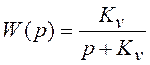 при случайном воздействии в виде винеровского процесса. В соответствии с (3.24)

.

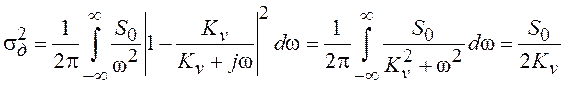2) С помощью апериодического звена  формируется экспоненциально-коррелированный процесс. Определим спектральную плотность мощности этого процесса.

. 

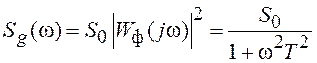Можно показать, что функция корреляции этого процесса имеет вид

.

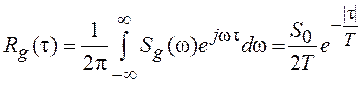 При проектировании радиолокационных и радионавигационных следящих измерителей используются модели движения с экспоненциально-коррелированными скоростью или ускорением. Процесс в этих моделях является нестационарным и для моделирования таких процессов необходимо применять временные методы.

3.8. Формирование случайных воздействий во временной области

Преимущество временной области заключается в том, что можно формировать нестационарные случайные процессы. При проектировании радиотехнических следящих измерителей широко используются модели изменения измеряемого параметра , скорость или ускорение которого являются винеровским или экспоненциально-коррелированным процессами. Моделируемый параметр  при этом является нестационарным случайным процессом.

Рассмотрим несколько примеров формирования таких процессов с помощью формирующего фильтра, на вход которого поступает белый шум со спектральной плотностью .