Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 9

Как видно из выражения (4.3), передаточная функция двигателя содержит кроме интегратора апериодическое звено с постоянной времени , обусловленное наличием момента инерции ротора. Постоянная времени зависит от конструкции двигателя. В коллекторных двигателях постоянного тока ротор имеет большую массу, и постоянная времени велика. В асинхронных двигателях переменного тока для снижения постоянной времени используют пустотелый ротор.

            Следящие системы с двигателем имеют большие размеры и стоимость. Поэтому в качестве интегратора широко применяется операционный усилитель с емкостной обратной связью (рис. 4.3, а). Определим функцию передачи этого устройства.

            Выходное напряжение равно

 ,                                                         (4.4)

где  – коэффициент усиления;  – входное напряжение.        

Полагая, что входной ток усилителя равен 0, из условия равенства токов в  и  получим,

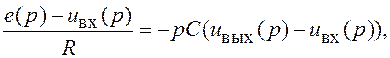                                     (4.5)

            Далее из (4.4) и (4.5) при  следует ПФ операционного усилителя:

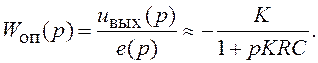                                             (4.6)

            Логарифмическая амплитудная частотная характеристика системы с функцией передачи (4.6) соответствует апериодическому звену с большой постоянной времени  (рис. 4.3,  б). В области частот выше значения

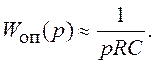
          Таким образом, свойства следящего измерителя с интегратором на операционном усилителе, зависящие от поведения ЛАЧХ в области высоких частот (полоса пропускания, свойства переходного процесса и запас устойчивости), не отличаются от свойств измерителя с идеальным интегратором.

          Но в области нижних частот () частотная характеристика (4.6) отличается от характеристики идеального интегратора и следящий измеритель с операционным усилителем имеет статическую ошибку. Вместе с тем эта ошибка невелика, так как коэффициент усиления операционного усилителя  составляет десятки тысяч.

          При цифровой реализации интеграторов используется приближенное представление операции интегрирования.

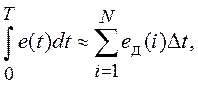
где  – дискретное время,  – интервал временной дискретизации, ,  – дискретизированный сигнал

          При цифровой обработке входной сигнал  в момент времени  подвергается квантованию по уровню в АЦП и заменяется дискретизированным значением . Ошибка квантования по уровню  при случайном сигнале  предполагается случайной величиной с равномерным распределением в интервале значений, соответствующем величине младшего разряда АЦП . При дальнейших расчетах ошибка квантования обычно представляется как аддитивный дискретный белый шум с дисперсией

          Действие интегратора в дискретном времени  можно описать  с помощью разностного уравнения

                                           (4.9)

Для реализации операций, содержащихся в (4.9), необходимо иметь элемент памяти, содержащий переменную , и устройство суммирования для добавления входной величины .     Эквивалентная схема дискретного интегратора представлена на рис. 4.4, а, осциллограмма выходного значения  при включении на вход постоянного сигнала  –  на рис. 4.4, б.

          При аппаратной реализации дискретного интегратора элемент памяти реализуется в виде регистра или счетчика. Если входная величина  представляется в виде последовательности импульсов со знаком, операцию суммирования можно реализовать в реверсивном счетчике импульсов, который в зависимости от знака суммирует или вычитает импульсы (рис. 4.4, в).

          При программной реализации элемент памяти интегратора реализуется в виде переменной  в памяти процессора. Например, в 16-разрядном сигнальном процессоре при использовании компилятора С переменную  можно представить как дробное число со знаком.

                                                        (4.10)

          Чтобы переходный процесс в интеграторе начался с нуля (как показано на рис. 4.4, б), в ячейку памяти  в соответствии с (4.10) загружается начальное значение 0. Эта операция выполняется после включения питания устройства при загрузке исполняемого файла программы в память процессора.