Точность и помехоустойчивость систем радиоавтоматики. Устройства радиоавтоматики, страница 23

Эффективная (шумовая) полоса системы  определяется частотной характеристикой замкнутой системы измерителя , а СПМ помехи  на входе системы зависит от вида измеряемого сигнала, типа дискриминатора и отношения мощностей сигнала и шума.

Для вычисления СПМ  дискриминатор представляется как линейное устройство с коэффициентом передачи  (рис. 4.31, б), и СПМ сигнала ошибки на выходе дискриминатора  пересчитывается   на вход  по формуле .

При использовании импульсных радиосигналов с периодом повторения  и действии шума необходимо определить дисперсию сигнала ошибки  или эквивалентную дисперсию измерения параметра   по одному импульсу. Тогда  СПМ ошибки измерения параметра на нулевой частоте равна

.                                                                (4.40)

          Расчет дисперсии  ошибки измерения параметра , содержащегося в радиосигнале, во многих случаях является сложной задачей, и на первоначальном этапе проектирования следящего измерителя целесообразно задаться потенциальной точностью измерения параметра. При оценке потенциальной точности параметр в течение длительности сигнала предполагается постоянным. В реальных устройствах точность измерения снижается из-за потерь, вызванных погрешностями реализации оптимальной схемы обработки сигналов. Однако при большом отношении мощностей сигнала и помехи  потери многих систем невелики и составляют 2-3 дБ.

Таблица 4.1

            При приеме смеси радиосигнала и широкополосного шума отношение сигнал/помеха q определяется выражением

,

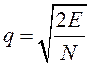где Е –  энергия принятого сигнала; N – cпектральная плотность мощности шума.

            Дисперсия минимальной ошибки измерения параметра сигнала равна

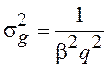,                                                       (4.41)

где  – среднеквадратическая характеристика параметра сигнала.

Значение  для различных измеряемых параметров приведено в табл. 4.1 [   ]. Прямоугольный импульс имеет бесконечную ширину спектра, поэтому при оценке точности предполагается, что ширина спектра ограничена полосой пропускания приемного тракта [    ]. 

Пример 4.2. Выполним расчет дисперсии отсчета временного положения сигнала, используемого в радионавигационной системе ГЛОНАСС. Отношение сигнал/помеха в зависимости от положения спутников меняется в пределах 30-50 дБ Гц. В канале широкого доступа используется псевдослучайная двоичная последовательность с периодом 1 мс, состоящая из 511 элементарных символов. Элементарный символ является прямоугольным импульсом длительностью  приблизительно 2 мкс. Спектр сигнала (и характеристика ) в рассматриваемом случае определяется спектром элементарного символа. Полоса пропускания приемного устройства  для повышения точности измерений в авиационной аппаратуре составляет 15 МГц.

Отношение сигнал/помеха 30 дБ Гц является отношением в дБ мощности сигнала к мощности помехи в полосе 1 Гц. 30 дБ Гц соответствует отношению мощностей  Гц. Чтобы получить квадрат отношения энергии к спектральной плотности , необходимо умножить  на длительность импульса .

          Тогда из табл. 4.1 и выражения (4.41) определим дисперсию измерения задержки по одному элементарному символу .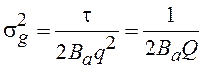

Период следования импульсов также равен , и спектральная плотность на нулевой частоте согласно (4.40) равна

.

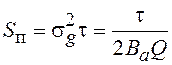Чтобы определить дисперсию флюктуационной ошибки следящего измерителя задержки, необходимо задаться эффективной полосой пропускания измерителя . При Гц получим