Импульсные и дискретные системы

 Импульсные и дискретные системы

8.1. Основные определения

Передача информации в радиотехнических системах может сопровождаться перерывами в силу различных причин:

- использование импульсной модуляции сигнала в радиоканале (например, использование амплитудно-импульсной модуляции – АИМ);

 - цифровая обработка радиосигналов, требующая дискретизации сообщений во времени (и квантования по уровню);

- воздействие на радиотехническую систему организованных помех.

          Прерывание информации в СУ моделируется специфическим звеном – импульсным элементом (ИЭ). Системы, содержащие ИЭ, будем называть импульсными. На входе ИЭ присутствует непрерывный сигнал x(t), а на выходе – последовательность импульсов x_и(t). Ограничиваемся случаем, когда ИЭ представляет собой линейный ключ, замыкающийся на время Δτ с периодом Δt (рис. 8.1, а). При этом на выходе ключа имеем амплитудно-модулированную последовательность импульсов (рис. 8.1, б).

          Если Δτ<< Δt, то ИЭ удобно представить в виде последовательного соединения идеального импульсного элемента (ИИЭ) и формирующего элемента (ФЭ), как показано на рис. 8.2, а. ИИЭ формирует последовательность δ-импульсов (рис. 8.2, б), модулированных по площади непрерывным сигналом x(t) (δ-импульсы имеют бесконечную амплитуду и единичную площадь):

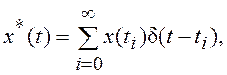                                                (8.1)

где t_i=iΔt, i=0,1,2,… .

          Функцию x^*(t) называют решетчатой.

          ФЭ преобразует δ-импульсы в последовательность импульсов заданной формы. Для прямоугольной формы импульсов (рис. 8.2, в) импульсную характеристику ФЭ можно представить в виде суммы двух ступенчатых функций, сдвинутых во времени на величину τ (), соответствующую длительности импульсов и имеющих различную полярность: 1(t)- 1(t- τ). При этом ПФ ФЭ записывается в виде:

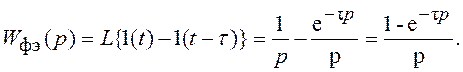
          Если τ=Δt, то ФЭ называют фиксатором нулевого порядка (ФЭ может также выполнять функцию линейного или параболического экстраполятора и, тогда, его называют фиксатором 1-го или, соответственно, 2-го порядка).

          В решетчатой функции x^*(t) используются только дискретные во времени значения непрерывного сигнала x(t). Если последующая обработка решетчатой функции в системе выполняется также в дискретном времени, то такую систему будем называть дискретной. При выполнении условия теоремы Котельникова для анализа дискретных систем применимы методы анализа непрерывных систем. Напомним,

что в разд. 1.13 было введено понятие дискретного эквивалента непрерывной системы, описание которого дано во временной области с помощью векторного разностного уравнения (1.37). В дальнейшем такое описание использовалось при анализе устойчивости (разд. 2), помехоустойчивости (разд. 3) и оптимизации дискретных систем. В отличие от непрерывных систем, для которых описание в частотной и временной области одинаково удобно, анализ дискретных систем проще выполнять во временной области. Тем не менее, описание  дискретных систем в частотной области иногда полезно (такая ситуация возникает, например, при построении частотных характеристик дискретных систем).

          Если последующая обработка решетчатой функции в системе выполняется в непрерывном времени (система содержит непрерывную часть с ПФ W_н(p)), то такую систему будем называть дискретно-непрерывной. Для анализа таких систем возможно применение методов анализа непрерывных систем, если величина 1/Δt существенно превышает полосу пропускания ее непрерывной части.

          Если время замыкания ключа Δτ соизмеримо с периодом Δt(рис. 8.1, б), то импульсную СУ будем называть системой с конечным временем съема данных. В зависимости от характера последующей обработки сигнала x_и(t) такие системы подразделяются на 2 класса: системы с конечным временем съема данных с непрерывной или дискретной обработкой сигнала. Например, следящий измеритель дальности в радиолокационной станции, работающей в режиме кругового обзора, представляет собой систему с конечным временем съема данных (время замыкания ключа Δτ зависит от ширины диаграммы направленности антенны в горизонтальной плоскости и периода обзора) с дискретной обработкой сигнала (интервал временной дискретизации определяется периодом повторения зондирующих импульсов).

          Существуют также более сложные СУ, в которых ИЭ не является линейным звеном (например, в случае широтной импульсной модуляции, когда от величины x(t) зависит длительность импульсов x_и(t), или в случае временной импульсной модуляции, когда значения x(t) определяют моменты возникновения импульсов x_и(t)). Кроме того, возможны ситуации, когда линейный ИЭ имеет переменный параметр Δt. Однако системы с подобными ИЭ, ввиду сложности их анализа, здесь не рассматриваются.

8.2. Решетчатые функции и z-преобразование