Импульсные и дискретные системы, страница 4

          Как указано в разд. 1.13, рассматриваемая дискретная система представляет собой простейший дискретный эквивалент непрерывной системы, безошибочно воспроизводящей воздействие g(t)=Vt. Структурная схема такой непрерывной системы показана на рис. 1.35, откуда легко определить ПФ в разомкнутом состоянии:

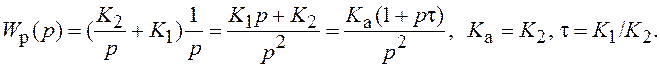
Частотная ПФ непрерывной системы в замкнутом состоянии имеет вид: 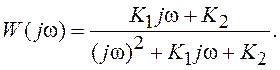    Для рассматриваемой дискретной системы в низкочастотной области (ω<<2π/Δt) выполняется условие z≈1+jωΔt и из (8.12) получаем

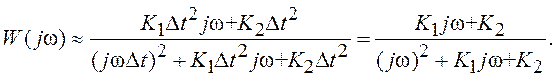
Частотные характеристики рассматриваемой непрерывной системы и ее простейшего дискретного эквивалента в низкочастотной области совпадают.

Замечание. Задача нахождения дискретного эквивалента непрерывной системы может решаться разными способами. В разд. 1.13 был рассмотрен способ нахождения простейшего дискретного эквивалента непрерывной системы на основе решения векторного дифференциального уравнения. В разд. 5 обсуждался синтез дискретной системы, структура которой согласована со структурой формирующего фильтра, представленного во временной области в дискретном времени. Задача проектирования дискретной системы может также решаться в частотной области с помощью ПФ. Например, известен способ нахождения дискретного эквивалента непрерывной системы по заданной импульсной характеристике. При этом ПФ дискретной системы определяется как z-преобразование импульсной характеристики непрерывной системы. Критерием эквивалентности такой дискретной системы и непрерывной системы-прототипа является равенство дискретных значений импульсной характеристики. Для других входных сигналов (кроме δ-функции) совпадение дискретных значений выходных сигналов не гарантируется. Известен также способ нахождения дискретного эквивалента непрерывной системы по заданной переходной характеристике. В этом случае ПФ дискретной системы определяется выражением:

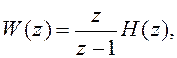
где H(z) – z-преобразование переходной характеристики непрерывной системы.

Результат полностью совпадает с простейшим дискретным эквивалентом, рассмотренным в разд. 1.13. Иногда для нахождения дискретного эквивалента используется билинейное преобразование: 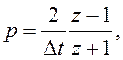 позволяющее от ПФ непрерывной системы перейти к ПФ дискретного эквивалента. Однако такой способ приводит к более сложной реализации дискретной системы.

          Полученные разными способами дискретные системы могут иметь различные частотные характеристики, разные области устойчивости и, даже, отличаться порядком астатизма. И только при очень малых значениях Δt они ведут себя примерно одинаково. В качестве иллюстрации дополним пример 2 решением еще 2-х аналогичных задач.

Пример 2а. Найдем ПФ и ЧХ дискретной системы, структура которой показана на рис. 1.36, б:

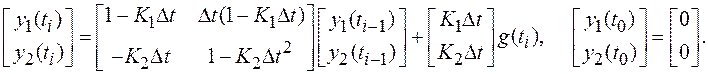
Если дискретная система, рассмотренная в примере 2, представляла собой простейший дискретный эквивалент непрерывной системы, согласованной со структурой непрерывного формирующего фильтра, содержащего 2 интегратора, то данная система согласована со структурой дискретного формирующего фильтра, также содержащего 2 интегратора (см. разд. 5). С помощью (8.10) нетрудно найти ПФ рассматриваемой системы:

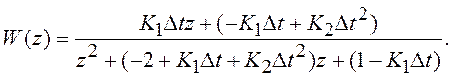                     (8.13)

Знаменатель ПФ (8.13) совпадает с левой частью характеристического уравнения  рассматриваемой системы и отличается от знаменателя ПФ (8.12). Заметим, что условия устойчивости дискретной системы (8.13) найдены в примере к разд. 2.6. Частотная ПФ системы 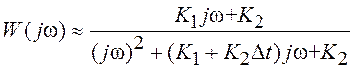  при ω<<2π/Δt  совпадает с результатом, полученным в примере 2 лишь в случае выполнения дополнительного ограничения на параметры системы: K₁>>K₂Δt.

          ПФ (8.13) получена с помощью (8.10) при условии, что выходным сигналом дискретной системы является запаздывающее значение y(t_i-1). Однако особенностью рассматриваемой дискретной системы является наличие линейной экстраполяции переменной y при формировании сигнала рассогласования (см. разд. 1.13). Поэтому здесь для вычисления ПФ целесообразно применить выражение (8.9):