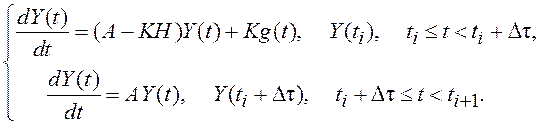 (8.20)
(8.20)
Уравнения (8.20) решаются методом «припасовывания», при котором решение 1-го уравнения в момент размыкания ключа Y(ti+Δτ) принимается в качестве начального условия для решения 2-го уравнения, а решение 2-го уравнения в момент замыкания ключа Y(ti+1) принимается в качестве начального условия для решения 1-го уравнения и т.д. При наличии случайных возмущений аналогичным образом решаются дисперсионные уравнения системы.
Для проверки устойчивости системы следует рассмотреть решения однородных дифференциальных уравнений. На момент размыкания ключа имеем
![]() (8.21)
(8.21)
На момент замыкания ключа имеем
![]() (8.22)
(8.22)
Подставляем (8.21) в (8.22): ![]() и результат рассматриваем как разностное уравнение
эквивалентной (для моментов времени ti) дискретной системы с переходной
матрицей
и результат рассматриваем как разностное уравнение
эквивалентной (для моментов времени ti) дискретной системы с переходной
матрицей ![]() . Далее выполняется анализ устойчивости
этой дискретной системы, имеющей характеристическое уравнение:
. Далее выполняется анализ устойчивости
этой дискретной системы, имеющей характеристическое уравнение: ![]()
Анализ системы с конечным временем съема данных и последующей дискретной обработкой сигнала выполняем для случая, когда структура системы представлена в виде, показанном на рис. 8.6.
Ключ периодически замыкается на время Δτ=nδt, кратное периоду дискретизации сигнала δt. Период замыкания ключа равен Δt=(n+m)δt (n и m – целые числа). Сигнал g(tk) поступает в дискретные моменты времени tk=kδt. Коэффициент K(t) изменяется в зависимости от состояния ключа:
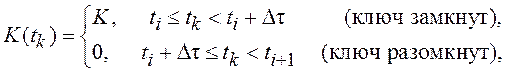
При замкнутом ключе рекуррентный алгоритм работы системы описывается векторным разностным уравнением
![]() (8.23)
(8.23)
Во время паузы соответствующее уравнение имеет вид:
![]() (8.24)
(8.24)
Уравнения (8.23) и (8.24) решаются совместно методом «припасовывания».
Проверка устойчивости системы выполняется следующим образом. Используя (8.23) при g(tk)=0 и (8.24) получим разностное уравнение системы для моментов размыкания ключа (эти моменты обозначим τi=ti+Δτ):
![]()
Из этого уравнения следует, что
исходную систему можно заменить эквивалентной дискретной системой с периодом
дискретизации Δt и переходной
матрицей ![]() . Далее выполняется анализ устойчивости
этой системы.
. Далее выполняется анализ устойчивости
этой системы.
В качестве примера выполним анализ устойчивости системы 2-го
порядка: 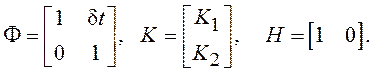
Характеристическое уравнение эквивалентной дискретной системы можно записать в виде:
![]()
где sp и det обозначают след и определитель матрицы Φэ.
В нашем случае 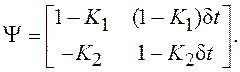
Для неравных собственных значений ψ1 и ψ2 матрицы Ψ с помощью теоремы Сильвестра найдем
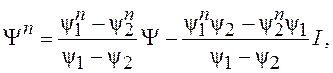 (8.25)
(8.25)
где 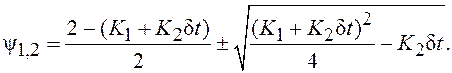
С учетом этого равенства и
соотношения 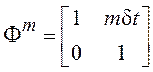 получим
получим
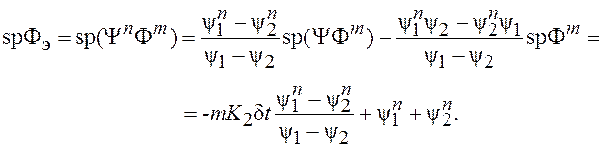 (8.26)
(8.26)
Определитель detΦэ находится по правилу произведения:
![]() (8.27)
(8.27)
Выражения (8.26) и (8.27) определяют коэффициенты характеристического уравнения эквивалентной дискретной системы. Для нахождения области параметров K1, K2, обеспечивающих устойчивость системы, можно применить алгебраический критерий. При m=0 и n=1 эта область показана на рис. 2.12. При больших паузах (m>>n) область устойчивости уменьшается и при m→∞ стягивается в точку K1=K2δt=1, соответствующую режиму максимального быстродействия или бесконечной степени устойчивости дискретной системы.
Для кратных собственных значений ψ1=ψ2=ψ
матрицы Ψ вместо (8.26) можно получить: ![]() причем
значение ψ связано с параметрами системы K1 и K2 соотношениями:
причем
значение ψ связано с параметрами системы K1 и K2 соотношениями:
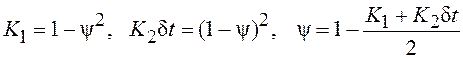 (этим значениям параметров
соответствует критический режим работы системы, разделяющий апериодические и
колебательные переходные процессы). Определитель detΦэ по-прежнему
находится с помощью (8.27). Применение алгебраического критерия устойчивости в
этом случае позволяет найти условие, определяющее максимальную допустимую длительность
паузы mгр, которая не нарушает устойчивости системы при
заданной продолжительности интервала съема данных n:
(этим значениям параметров
соответствует критический режим работы системы, разделяющий апериодические и
колебательные переходные процессы). Определитель detΦэ по-прежнему
находится с помощью (8.27). Применение алгебраического критерия устойчивости в
этом случае позволяет найти условие, определяющее максимальную допустимую длительность
паузы mгр, которая не нарушает устойчивости системы при
заданной продолжительности интервала съема данных n:
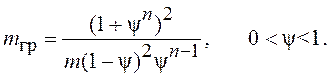
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.