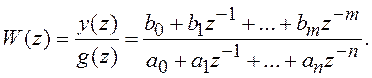Импульсные и дискретные системы, страница 3

                                 (8.6)

          ПФ дискретной системы выполняет ту же роль, что и ПФ непрерывной системы. Однако основным ее предназначением является построение частотных характеристик дискретной системы (анализ показателей качества дискретных систем проще выполнять во временной области). Заметим, что соотношение порядков многочленов по отрицательным степеням z в числителе и знаменателе (8.6) не влияет на условия физической реализуемости и может быть произвольным (при любом выборе n и m в уравнение (8.5) не входят будущие значения g и y). Однако значения коэффициентов a₀,…,a_n и b₀,…,b_mне могут быть произвольными (реакция системы не должна зависеть от более поздних воздействий). Знаменатель ПФ – есть левая часть характеристического уравнения системы. Связь ПФ дискретной системы в замкнутом и разомкнутом состоянии устанавливается, как и для непрерывных систем, с помощью соотношения .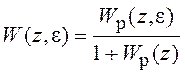

Если ПФ дискретной системы в разомкнутом состоянии W_р(z) имеет в точке z=1 полюс кратности r, то порядок астатизма системы равен r и дискретные значения ошибки равны нулю при входном воздействии вида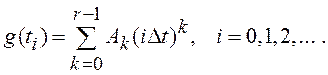

          Частотная ПФ дискретной системы получается из ПФ W(z) заменой:   Частотные характеристики дискретной системы периодичны и их значения повторяются с периодом 2π/Δt (дискретные функции на частотах ω и ω±2πi/Δt , i=1,2,… неразличимы и дискретная система реагирует на них совершенно одинаково). Для выделения низкочастотного фрагмента частотных характеристик дискретной системы на ее входе обычно включают аналоговый фильтр.

          Пусть система описана в пространстве состояний:

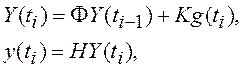                                        (8.7)

где Φ, K и H – некоторые матрицы; начальные условия полагаем нулевыми.

          Применяем к уравнениям (8.7) z-преобразование:

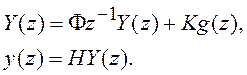
Из 1-го уравнения находим  и подставляем во 2-е уравнение:

                                            (8.8)

          В соответствии с данным ранее определением ПФ дискретной системы (8.6) имеем

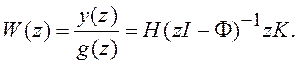                                      (8.9)

          Заметим, что (8.8) можно записать иначе:

 и если выходным сигналом дискретной системы является запаздывающее значение y(t_i-1), то связь описаний дискретной системы в частотной и временной области определяется так же, как и для непрерывной системы (1.36):

                                                 (8.10)

При этом запаздывание выходного сигнала не влияет на вид АЧХ дискретной системы.

Пример 1. Найдем ПФ и ЧХ дискретной системы 1-го порядка (1.39):

К этому разностному уравнению применяем z-преобразование:

Полагаем, что выходным сигналом системы является y(t_i-1), тогда

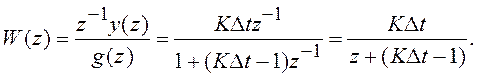
ПФ системы в разомкнутом состоянии равн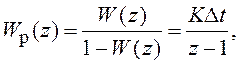а  следовательно дискретная система имеет 1-й порядок астатизма.

          Для определения частотной ПФ выполняем замену :

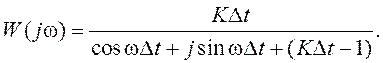                          (8.11)

При построении частотных характеристик можно воспользоваться вычислительными средствами (например, средствами MatLab). Как указано в разд. 1.13, рассматриваемая дискретная система представляет собой простейший дискретный эквивалент непрерывной системы с ПФ в разомкнутом состоянии  и частотной ПФ в замкнутом состоянии 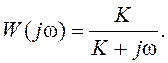 Рассмотрим низкочастотный фрагмент (8.11) при ω<<2π/Δt. При этом cosωΔt≈1 и sin ωΔt≈ ωΔt. Получаем из (8.11):

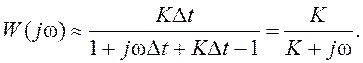
Частотные характеристики рассматриваемой непрерывной системы и ее простейшего дискретного эквивалента в низкочастотной области совпадают.

Пример 2. Найдем ПФ и ЧХ дискретной системы 2-го порядка (1.45):

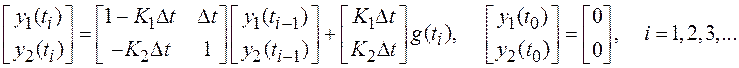С целью вычисления ПФ воспользуемся выражением (8.10) при

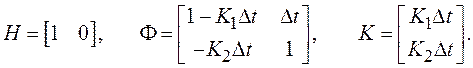
Обращение матрицы выполняется по формуле:

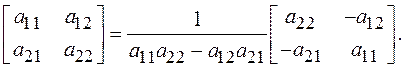
Результат:  

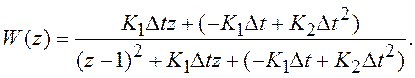                     (8.12)

ПФ системы в разомкнутом состоянии равн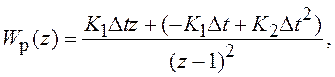а  следовательно дискретная система имеет 2-й порядок астатизма.

          Для определения частотной ПФ следует выполнить замену .