Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 8

Если числитель и знаменатель в выражении для числа Прандтля умножить на плотность, то 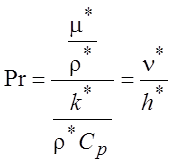. Здесь n* - кинематическая вязкость газа, характеризующая скорость передачи импульса, а h* - коэффициент температуропроводности, характеризующий скорость передачи тепла. Таким образом, число Прандтля это отношение скоростей передачи импульса и тепла. Для воздуха Pr = 0,72, а для жидких металлов и плазмы оно может быть много меньше единицы, так как импульс в них передается атомами или ионами, а тепло гораздо более быстрыми электронами.

Из первого уравнения системы (1.45) можно сделать еще одно важное заключение. Одной из типичных задач аэрогидродинамики является задача обтекания покоящегося тела. Граничные условия для нее будут u’_i =0 на поверхности и u’₁ = 1, u’₂ = u’₃ = 0 на бесконечности. Для геометрически подобных границ скорости u’_i являются функциями только x’_i и Re. Из этого следует, что решения для течений вдоль подобных границ будут идентичны по форме независимо от рода жидкости, если только числа Рейнольдса одинаковы. Подобие течений по числу Рейнольдса позволяет моделировать условия обтекания тела в малоразмерных установках, подбирая жидкость подходящей вязкости.

2.  ПРИМЕРЫ ТОЧНОГО РЕШЕНИЯ УРАВНЕНИЙ ДИНАМИКИ ВЯЗКОГО ГАЗА

Уравнения динамики вязкого газа – нелинейные уравнения, общий метод решения которых пока не найден. Исключение составляют несколько простейших случаев движения вязкой несжимаемой жидкости, для которых можно пренебречь влиянием нелинейных членов и получить точные решения. К таким течениям относятся движения жидкости, в которых отличается от нуля только одна компонента скорости, зависящая от одной координаты. Их называют слоистыми.

2.1.  Обобщенное течение Куэтта

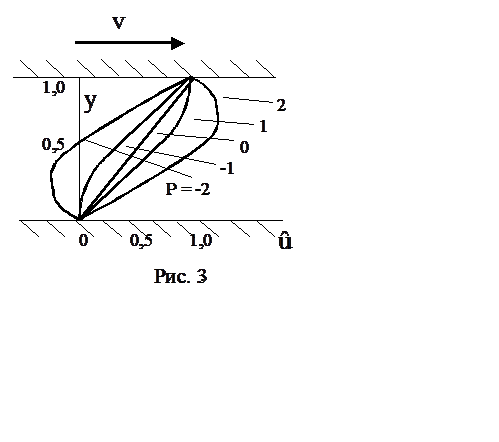Пусть несжимаемая жидкость заключена между двумя параллельными плоскостями, одна из которых движется относительно другой с постоянной скоростью V на расстоянии h (рис.3). За плоскость x, z примем неподвижную плоскость, а ось x направим по направлению . Рассмотрим течение, в котором отличается от нуля только одна компонента скорости – u. Выпишем уравнения движения для этого случая и поставим граничные условия.

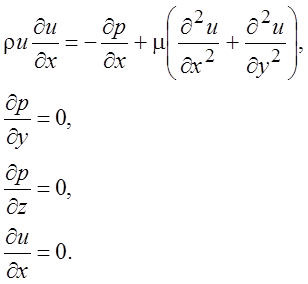                            (2.1)

u = 0   при  y = 0;   u = V  при   y = h.                                         (2.2)

Из уравнения неразрывности (четвертое уравнение) следует, что скорость u не зависит от координат х и z, а зависит только от координаты y. Поэтому в первом уравнении первый член в скобках равен нулю. Из второго и третьего уравнений движения следует, что 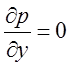;  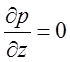или p = p(x). Первое из уравнений движения дает следующую зависимость:

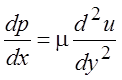.                                                      (2.3)

В уравнении (2.3) правая часть зависит только от y, левая – только от x. Это возможно лишь при условии, если левая и правая части являются постоянными величинами. Таким образом,

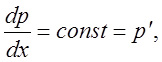
и давление является линейной функцией координаты x. Для скорости из (2.3) получим следующее общее решение:

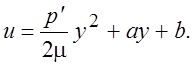                                                       (2.4)

Постоянные a и b определим из граничных условий (2.2).

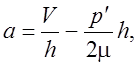  b = 0.                                         (2.5)

подставив (2.5) в (2.4), получим решение задачи:

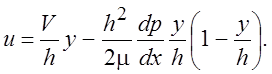                                  (2.6)

Введем безразмерные градиент давления, скорость и координату:

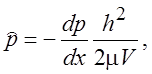
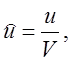
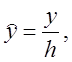                                        (2.7)

тогда

                                                (2.8)

Течение с профилем скорости (2.6) получило название обобщенного течения Куэтта. Средняя по толщине слоя скорость жидкости , где Q – расход жидкости, S – поперечное сечение канала. Для рассматриваемого случая

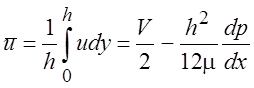.                                             (2.9)

Сила трения, действующая на неподвижную плоскость,

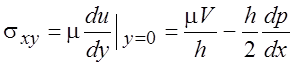.                                        (2.10)