Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 6

.                                                  (1.24)

Коэффициент k называется коэффициентом теплопроводности, который в общем случае зависит от температуры и давления. Знак минус указывает на то, что направление теплового потока обратно направлению увеличения температуры. Изменение тепла в элементарном объеме будет определяться интегралом

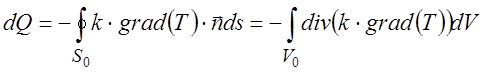.                      (1.25)

Тогда подвод тепла в объем в единицу времени за счет теплопроводности дается соотношением

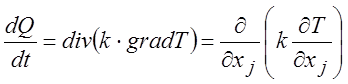.                                (1.26)

Полная работа dA, совершаемая над объемом газа V₀, образуется в результате действия касательных сил и сил давления (нормальных к поверхности сил). Поток энергии через поверхность этого объема, связанный с этими силами, определяется произведением этих сил на скорость. Его компонентами будут величины e_j = u_i×t_ij. Общий поток энергии внутрь объема, производимый поверхностными силами будет

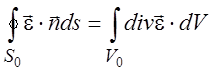                                          (1.27)

т.е. над объемом V₀ в единицу времени поверхностные силы выполняют работу

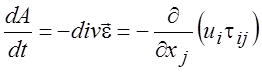.                                  (1.28)

Здесь учтено, что работа, совершаемая над газом, считается отрицательной, а совершаемая газом - положительной.

Изменение кинетической энергии в единицу времени можно записать как

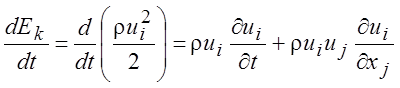.                        (1.29)

Члены справа в (1.29) можно выразить, используя уравнение Навье-Стокса (1.20).

                                                   .

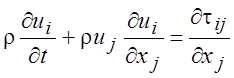Умножив его на скорость u_i, мы получим выражение для баланса мощности или изменения энергии во времени, так как уравнение (1.20) по определению есть уравнение баланса сил:

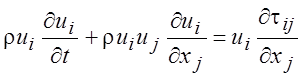                                         .                                      (1.30)

Тогда

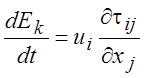                                                   .                                                   (1.31)

Подставив выражения (1.26), (1.28) и (1.31) в уравнение (1.23) получим

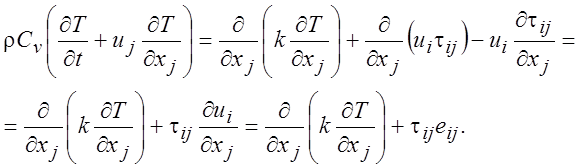          (1.32)

Окончательно

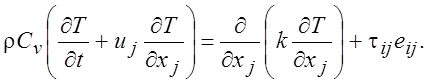                                (1.33)

Уравнение энергии (1.33) для идеального газа зачастую представляют в несколько измененном виде. Продифференцировав по времени уравнение состояния идеального газа p/r =RT = (C_p – C_v)T получаем

.

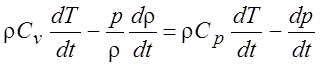Принимая во внимание уравнение неразрывности (1.7), из которого следует, что 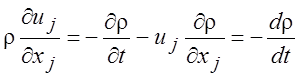, можно показать справедливость соотношения

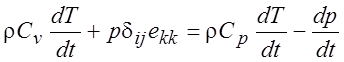,  где 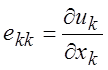.                     (1.34)

Учитывая (1.34), уравнение энергии (1.33) можно преобразовать к виду

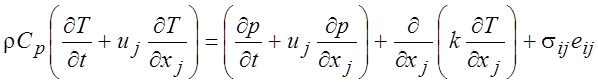.         (1.35)

Таким образом, тепловой баланс объема жидкости описывается уравнениями (1.32) или (1.35). В них входят члены, которые определяют: изменение внутренней энергии (член слева); изменение тепла за счет теплопроводности (второй член справа); работу нормальных (первый член справа) и касательных напряжений (последний член справа).

1.4.  Замыкание уравнений движения

Для замыкания системы уравнений движения газа используются соотношения, характеризующие термодинамическую природу изучаемой среды, называемые законами состояния. В общем случае они задают связь между давлением, температурой и плотностью

.                                             (1.36)

Для идеального газа уравнением состояния является уравнение Клапейрона:

                                                              ,                                                (1.37)

где R - газовая постоянная.

За седьмое замыкающее уравнение можно взять эмпирическую связь между коэффициентом вязкости и температурой

                                                  (1.38)

В качестве такой связи может быть степенная зависимость

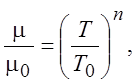                                                     (1.39)

где степенной показатель в зависимости от температуры газа может лежать в диапазоне .