Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 18

Уравнение (5.8) было решено Хартри (Hartree, 1937). Некоторые из полученных им результатов приведены на рис.13. Для ускоренного течения (m > 0, b > 0) профили скорости не имеют точек перегиба. Для замедленного течения (m < 0, b < 0) точки перегиба есть. Отрыв пограничного слоя происходит при b = - 0, 1908 (m= - 0, 091). Отсюда следует, что ламинарный пограничный слой может прилегать к телу без отрыва только при малых замедлениях течения.

5.2.  Задача Блазиуса

Из всех частных случаев распределения (5.1) особое значение имеет случай с m = 0. Он  соответствует равномерному потоку, омывающему полубесконечную пластину (Blasius, 1908). Для того чтобы точно соответствовать решению Блазиуса, исключим из замены (5.7) множитель 2. Тогда из (5.8) мы получим следующее обыкновенное дифференциальное уравнение

                                                      (5.10)

с граничными условиями

; .                                (5.11)

Блазиус получил решение задачи (5.10) – (5.11), применив разложение функции f(h) в ряд в окрестности h = 0 и асимптотическое разложение для h = ¥, сшив эти разложения в некоторой подходящим образом выбранной точке.

В настоящее время проинтегрировать уравнение (5.10) численно не составляет труда. Некоторое неудобство создает то, что граничные условия заданы на различных  концах интервала. Для того чтобы поставить задачу Коши, необходимо знать значение . Для нахождения  можно использовать какой-либо из вариантов прогонки, перенеся граничное условие из ¥ в некоторую точку, расположенную на расстоянии d от поверхности тела. Значение d можно уточнить в процессе расчетов так, чтобы  и время счета было приемлемым.

Решение задачи (5.10), (5.11) дает  = 0,332.

Касательное напряжение на пластине в соответствии с (4.21)

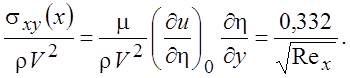                                         (5.12)

здесь  - переменная Блазиуса;  - число Рейнольдса.

Сопротивление на обеих сторонах пластины длиной l и шириной b получим по формуле (4.23)

                            (5.13)

Коэффициент сопротивления

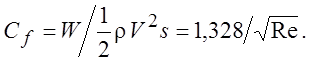                                      (5.14)

Выражение (5.14) – закон Блазиуса для сопротивления продольно обтекаемой пластинки. Он применим только для ламинарного течения.

Определим характерные толщины пограничного слоя. Расчеты показывают, что толщина пограничного слоя  толщина вытеснения  а толщина потери импульса .

В заключение отметим, что решение Блазиуса в разные времена неоднократно подтверждалось измерениями.

6.  ПРИБЛИЖЕННЫЕ ОДНОПАРАМЕТРИЧЕСКИЕ

МЕТОДЫ

Во многих задачах аэронавтики и гидротехники требуются быстрые методы расчета, дающие возможность оценить характеристики пограничного слоя, не прибегая к громоздким аналитическим или численным вычислениям. В данном параграфе мы рассмотрим однопараметрические методы, основанные на интегральной форме записи уравнений пограничного слоя. В настоящее время они во многом потеряли свою актуальность, но, по-крайней мере, представляют историческую ценность, показывая, как даже в отсутствие точных методов человеческий разум может получать надежные данные, используя общие положения и немного изобретательности.

Основная идея приближенных однопараметрических методов состоит в том, чтобы аппроксимировать профили скорости некоторыми функциями с одним параметром (формпараметром). Этот параметр является функцией продольной координаты и указывает, к какому сечению надо отнести приближенный профиль. Зависимость параметра от продольной координаты получают из интегрального условия, вытекающего из теоремы импульсов.

6.1.  Интегральное условие импульсов

Рассмотрим установившийся двумерный поток, для которого уравнения пограничного слоя имеют вид (4.17). Умножим уравнение неразрывности на u и сложим с уравнением (4.17). Получим

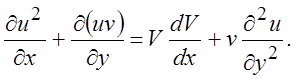                                     (6.1)

Умножим уравнение неразрывности на V. После преобразования запишем его в виде

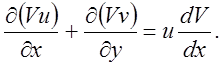                                                   (6.2)