Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 7

Показатель n = 0,5 соответствует взаимодействию молекул в виде твердых шаров, когда скорость обмена импульсом между молекулами зависит только от их скорости, которая пропорциональна корню из температуры газа, и хорошо описывает вязкость при высокой температуре газа. Выражение (1.39) с n = 1 - хорошо описывает поведение вязкости для T < 50K, когда в процессе обмена импульсом участвует не только отталкивающая часть потенциала взаимодействия между молекулами, но и притягивающая часть. С понижением энергии (температуры) молекул растет эффективное сечение взаимодействия молекул. Для воздуха достаточно хорошей аппроксимацией в широком диапазоне температур будет связь (1.39) с n = 0,76. Часто связь коэффициента вязкости и температуры задают формулой Сатерленда

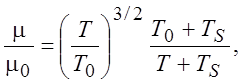 где .                       (1.40)

Здесь m₀ и T₀ соответствуют некоторому начальному состоянию газа.

1.5.  Граничные и начальные условия

Система уравнений (1.7), (1.18), (1.33), (1.36) и (1.38) имеет бесчисленное множество частных решений, которые не всегда соответствуют реальному течению газа. Практический смысл имеет отыскание таких решений, которые соответствуют рассматриваемому течению. Для этой цели задаются граничные и начальные условия.

Уравнения движения газа содержат производные по времени, поэтому в общем случае необходимо задать начальное распределение всех входящих в задачу величин в момент времени t =0 во всем объеме. Например, для скорости мы должны знать

                                             (1.41)

Если твердое тело движется в газе и задано уравнение его поверхности как

,                                             (1.42)

то кинематическое условие, отражающее тот факт, что газ не пересекает эту поверхность, а скорость газа на поверхности тела совпадает со скоростью перемещения его поверхности, записывается в виде

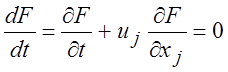.                                       (1.43)

Условие (1.43) для вязкого газа означает, что частицы жидкости, находящиеся в непосредственной близости от поверхности тела, к ней “прилипают”. Поэтому можно потребовать, чтобы в системе, связанной с телом, на поверхности тела u_i = 0.

Граничные условия для температуры допускают большее разнообразие, чем для скорости. На поверхности обтекаемого газом тела можно задать температуру (постоянную или переменную) или поток тепла через поверхность.

Вне тела задаются условия на бесконечности, которые отражают тот факт, что вдали от тела течение не возмущено и все параметры соответствуют невозмущенному течению.

1.6.  Безразмерная запись уравнений движения

Примем, что течение газа характеризуется следующими масштабными величинами длины, скорости, температуры, плотности и вязкости: L*, V*, T*, r*, m*. Условимся отмечать в этом параграфе штрихом соответствующие безразмерные переменные:

          (1.44)

Подставив (1.44) в уравнения движения вязкого газа, мы получим безразмерную запись уравнений:

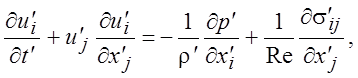
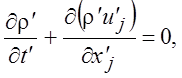
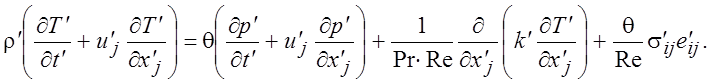                     (1.45)

Видно, что в систему уравнений (1.45) входит три безразмерных параметра:

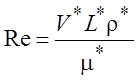 - число Рейнольдса;

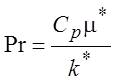 - число Прандтля;

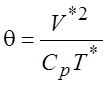 - температурный критерий или критерий Эккерта.

Видно, что температурный критерий q является отношением кинетической энергии к внутренней энергии в потоке. Если учесть, что С_р = gR /(g - 1), то 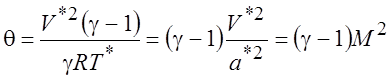. Положение температурного критерия в уравнении энергии (1.45) и его связь с числом Маха показывает, что теплота, возникающая вследствие трения и сжатия, становится существенной только в тех случаях, когда скорость течения становится сравнимой со скоростью звука.

Особую роль в задачах, представленных в учебнике, играет число Рейнольдса Re. Если числитель и знаменатель в соотношении для него умножить на V*, то 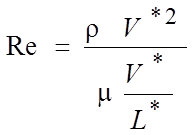 и оно физически отражает соотношение сил инерции и вязкости. Фактически, здесь мы будем рассматривать различные предельные случаи очень больших или очень малых чисел Рейнольдса.