В дальнейшем будет встречаться еще одна условная толщина слоя – толщина потери импульса d**. Она задается выражением
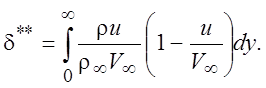(4.19)
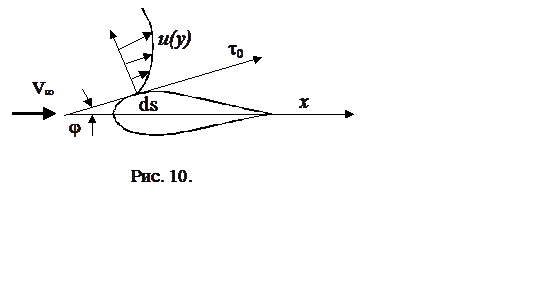Легко показать, что через отрезок d** в отсутствие пограничного слоя проходило бы
количество движения, равное потере импульса в пограничном слое из-за торможения
газа, то есть толщина потери импульса тесно связана с величиной сопротивления
тела. Вычисление сопротивления тела при его движении в газе является одной из
основных задач динамики вязкого газа. Оно определяется касательным напряжением
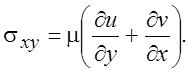(4.20)
Так как 
, в выражении (4.20) останется только
основной член
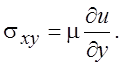(4.21)
Для вычисления сопротивления следует проинтегрировать выражение (4.21) на стенке по всей поверхности тела.
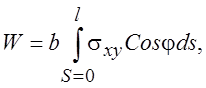(4.22)
здесь l - высота обтекаемого цилиндрического тела; b - его ширина; j - угол, образуемый касательной к поверхности тела с направлением скорости V набегающего потока; s - координата, измеряемая вдоль поверхности тела (рис. 8).
Так как Cos j ds = dx, где координата x направлена по скорости V, выражение (4.22) можно записать в виде
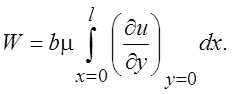(4.23)
Таким образом, для вычисления сопротивления трения необходимо знать градиент скорости на стенке.
4.4. Отрыв пограничного слоя
Потеря энергии и количества движения в пограничном слое приводит к замедлению потока и утолщению пограничного слоя. Если есть область возрастания давления, то поток в конце концов остановится, пограничный слой оторвется от поверхности. В точке отрыва касательное напряжение становится равным нулю, так что
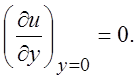
За точкой отрыва возникает медленное возвратное течение (рис. 11).
Отрыв пограничного слоя возможен только в зоне замедляющегося течения,
т.е. в зоне с 
. Действительно, в точке отрыва
профиль скорости должен иметь точку перегиба. Покажем, что появление точки
перегиба возможно только при возрастании давления. Обратим внимание на то, что
вторая производная скорости у внешней границы пограничного слоя всегда
отрицательна. На поверхности тела, как это следует из уравнений Прандтля и
граничных условий, выполняется следующее равенство:
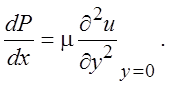(4.24)
Если
течение разгоняется, то 
. И, как следует из (4.24),
также меньше нуля на стенке, а значит, и
везде в пограничном слое. Отсюда вытекает, что точки перегиба нет. Для
замедляющего течения 
и
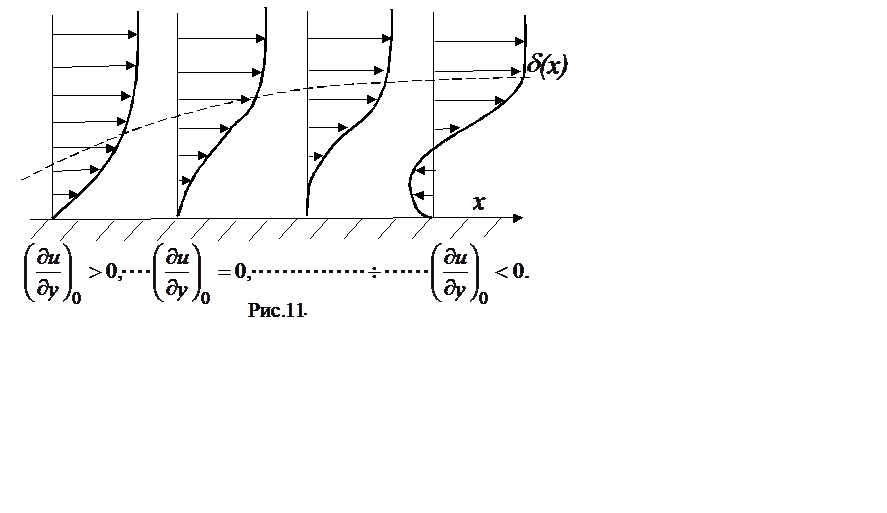
> 0 на стенке и,
значит, где-то в слое, где = 0, должна быть
точка перегиба, а стало быть, и отрыв пограничного слоя.
Следует подчеркнуть, что уравнения пограничного слоя справедливы только до точки отрыва, за которой – область, где течение формируется за счет вязкости, значительно возрастает, и не выполняются основные предположения, положенные в основу вывода уравнений пограничного слоя. Вследствие образования ниже по течению завихренного следа сильно увеличивается общее сопротивление. Поэтому предсказание точки отрыва чрезвычайно важно и его можно делать, основываясь на теории пограничного слоя.
4.5. Область применимости уравнений
пограничного слоя
Приведенное в предыдущем пункте ограничение, связанное с отрывом пограничного слоя, не является единственным. Так как уравнения пограничного слоя выведены в предположении малости толщины пограничного слоя, т.е. для больших чисел Рейнольдса, само собой разумеется, что они не справедливы в окрестности передних кромок. Но и при больших числах Рейнольдса их надо применять с известной долей осторожности. Выведенные уравнения описывают ламинарные течения. При больших же числах Re течение переходит в турбулентное состояние, которое описывается другими уравнениями. Они будут рассматриваться ниже.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.