Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 4

Рассмотрим некоторый достаточно малый объем пространства V₀, в котором можно предположить, что все характеристики жидкости однородны. Через элемент поверхности ds, ограничивающий объем V₀, протекает в единицу времени  газа. Вектор  по абсолютной величине равен площади элемента поверхности и направлен по внешней нормали к ней. Полное количество газа, вытекающего в единицу времени из объема V₀, через площадь его ограничивающую равно m.

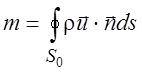                                                 .                                          (1.1)

В то же время, масса газа в этом объеме есть 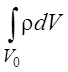. Уменьшение количества газа в объеме V₀ можно представить в виде

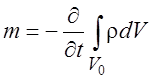                                                 .                                         (1.2)

Приравняв выражения (1.1) и (1.2), получаем

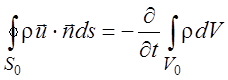                                                 .                              (1.3)

Преобразуем интеграл по поверхности в интеграл по объему по формуле Гаусса-Остроградского и получим

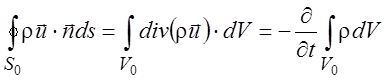                                                          (1.4)

или

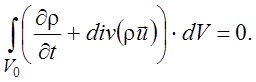                                                                            (1.5)

Так как соотношение (1.5) должно выполняться для любого объема с однородными параметрами внутри, подынтегральное выражение должно быть равно нулю:

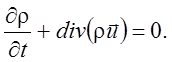                                                                                        (1.6)

Это и есть уравнение неразрывности.

В тензорном представлении, где по повторяющемуся индексу подразумевается суммирование, уравнение неразрывности будет иметь вид

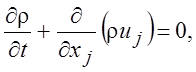                                           где                        (1.7)

1.2.  Уравнения Навье-Стокса

Уравнение сохранения количества движения можно получить из второго закона Ньютона, примененного к элементарному объему газа. Предположим, что на элементарный объем действуют внешние объемные (массовые) силы - F_i и поверхностные силы - P_i . Тогда, согласно второму закону механики

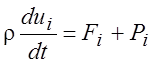                                                   .                                                 (1.8)

Полная, или субстанциональная производная  определяет изменение скорости передвигающейся в пространстве частицы газа. Это изменение складывается из двух частей: из изменения скорости в данной точке пространства за время dt и из разности скоростей в двух точках, расположенных на расстоянии, которое прошла рассматриваемая частица за этот период времени. Выражение для субстанциональной производной легко получить прямым дифференцированием

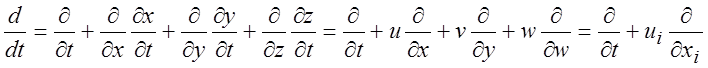.                     (1.9)

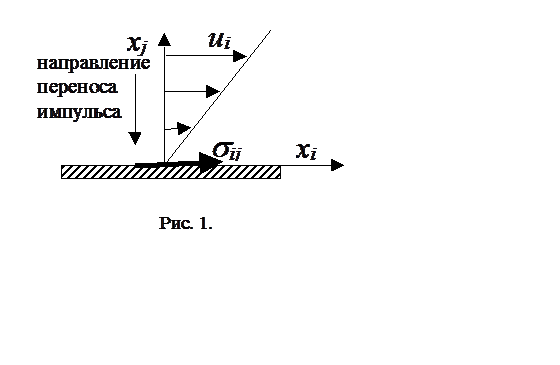Величина силы Р_i, действующая на элементарный объем жидкости, складывается из действия скалярных сил давления р на поверхность и сил связанных с вязкостью жидкости s_ij, которые действуют по касательной к поверхности. Совокупность сил P_i определяет напряженное состояние в потоке. Необходимо связать его с деформированным состоянием, т.е. надо выразить поверхностные силы через компоненты скорости (или их производные) и давление.

Под действием сил давления в газе осуществляется чисто обратимый перенос импульса, связанный с механическим перемещением различных объемов газа из одного места в другое. В случае вязкого газа появляется еще дополнительный перенос импульса из мест с большей скоростью в места с меньшей, вызванный наличием внутреннего трения (см. рис.1). Из рисунка видно, что вязкие силы s_ij – это напряжения, действующие вдоль оси x_i на площадку, нормальную к оси x_j. Девять компонент s_ij образуют тензор вязких напряжений второго ранга. Полная сила Р_i, действующая на выделенный объем газа V₀ , равна

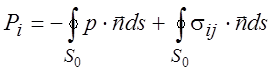,                                     (1.10)

Преобразуем выражение (1.10) в интеграл по объему

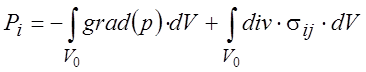  .                              (1.11)

Тогда на объем V₀ действует сила

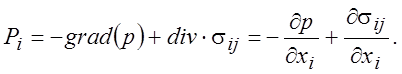                                (1.12)

Деформация элемента газа под действием сил s_ij определяется только градиентами скорости , так как при равномерном движении вязкое трение отсутствует, а производными более высоких порядков можно пренебречь. Это является одним из основных допущений при выводе уравнений Навье-Стокса. Выделим в тензоре  симметричную и антисимметричную части: