Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 19

Вычтем из (6.2) уравнение (6.1) и проинтегрируем полученное равенство от 0 до ¥ по y.

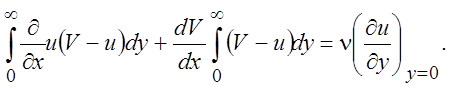                     (6.3)

Здесь использовано обращение в нуль величины u(V – u) при подстановке пределов интегрирования, следующее из граничных условий, и асимптотическое стремление к нулю производной  при y ® ¥.

Вспоминая выражения для толщин вытеснения и потери импульса (4.18) и (4.19), допуская возможность замены порядка интегрирования и дифференцирования, вводя напряжение на стенке согласно (4.21), мы получим интегральное условие Кармана (уравнение импульсов):

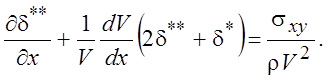                                    (6.4)

6.2.  Метод Кармана – Польгаузена

Польгаузен (Pohlhausen, 1921) предложил использовать в уравнении (6.4) зависимость u(y) в виде полинома четвертой степени

,  ,  i = 0,….,4.                                       (6.5)

Константы  определим из граничных условий

;  ;  ;                                  (6.6)

и дополнительного условия, которое дает уравнение Прандтля при y = 0:

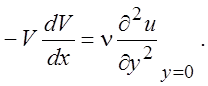                          (6.7)

Условие (6.7) можно представить в виде

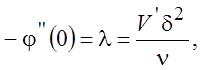                                 (6.8)

здесь l - формпараметр Польгаузена.

Решение системы (6.6), (6.8) дает

                     (6.9)

Тогда распределение скорости можно записать в виде

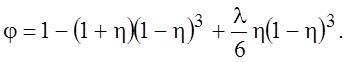                                    (6.10)

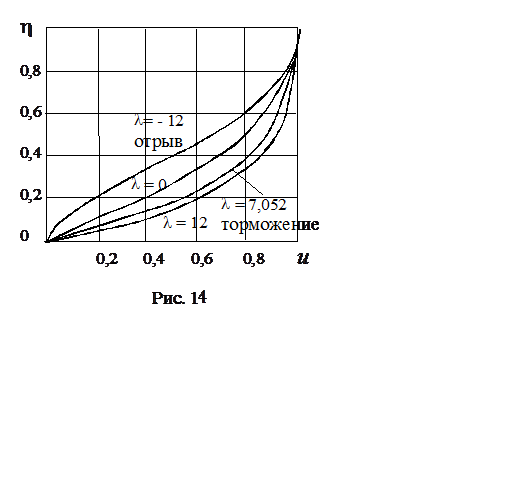Определим границы применимости формулы (6.10). Отрыв пограничного слоя  происходит, когда  при y = 0. Это условие дает следующее ограничение: l ³ -12. Условие монотонного роста скорости (условие u/V £ 1 или 0 £ h £ 1) накладывает на l еще одно ограничение: l £ 12. Профили скорости для диапазона –12 £ l £ 12 приведены на рис. 14.

Составим уравнение для определения l(x), используя уравнение импульсов (6.4). Вычислим

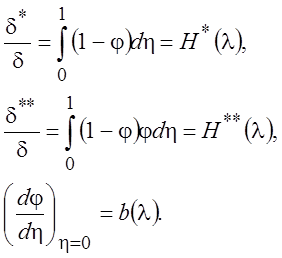                                (6.11)

Тогда уравнение (6.4) можно записать в виде

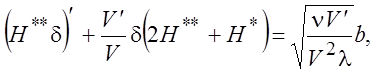                                                              (6.12)

которое, в свою очередь, можно представить как

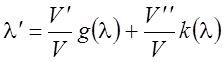                                         .                                                  (6.13)

Уравнение (6.13) дает общий вид преобразованного уравнения импульсов в случае однопараметрического набора профилей. Его необходимо проинтегрировать численно от х = 0. Функции g(l) и к(l) затабулированы, однако интегрирование вызывает определенные сложности из-за особых точек в начале координат и в точке минимума давления. Условие монотонности роста скорости (производная скорости не должна иметь нулей внутри интервала 0<h<1, за исключением границ) накладывает на l еще одно ограничение. Из условия 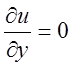 при y>1 получим, что l £ 12. Отметим, что эти ограничения справедливы для двумерных пограничных слоев. В случае трехмерного течения условие монотонности может нарушаться. Например, немонотонные профили скорости возникают в продольном направлении на крыльях со скольжением.

Установлено, что метод Кармана-Польгаузена дает хорошие результаты для ускоряющихся (конфузорных) течений, но менее удовлетворительно описывает замедляющиеся (диффузорные) течения. Профили скорости, полученные по этому методу, отстают от точных профилей в развитии, положение отрыва затягивается, иногда даже пропадает. В целом можно констатировать, что метод Кармана-Польгаузена оказался сложным и недостаточно точным. Было создано много других однопараметрических методов, использующих идею метода Кармана-Польгаузена, гораздо более простых и точных.

Задача 6.1.

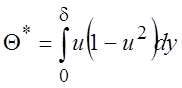Определить толщину потери энергии в пограничном слое , где u = u*/U. Вывести уравнение для Q*(х).

Задача 6.2.

Рассчитать пограничный слой на пластине приближенно. Апроксимировать распределение скорости в пограничном слое выражением u = ASin(By+C).

Задача 6.3.

Рассчитать пограничный слой в критической точке приближенно. Апроксимировать распределение скорости в пограничном слое полиномом второй степени.

Задача 6.4.

Применить метод Польгаузена для течения над плоской пластиной V(x) = V, получить интегральные характеристики пограничного слоя.