Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 15

Для газов число Прандтля близко к единице, то есть толщина температурного пограничного слоя действительно одного порядка с толщиной динамического.

Оценка остальных членов в уравнении (1.35) показывает, что в диссипативной функции следует сохранить только члены и . Следовательно,

                                          (4.11)

Таким образом, тепло, возникающее вследствие трения, существенно только при условии , тогда член

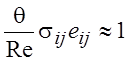                                                         (4.12)

будет одного порядка с членами, зависящими от конвекции и теплопроводности.

Учитывая проведенные оценки, уравнение энергии для пограничного слоя можно представить в следующем виде:

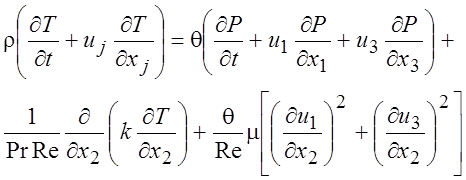.                         (4.13)

Возвращаясь к размерным величинам, выпишем уравнения плоского стационарного пограничного слоя в общепринятых обозначениях:

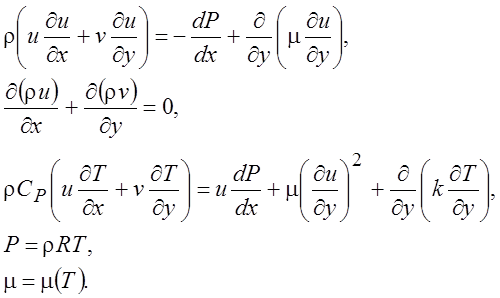                     (4.14)

В полученной системе содержится пять уравнений и пять неизвестных: r, u, v, T, m.

4.2.  Уравнения Прандтля

Для несжимаемой среды (r = const, М = 0) и для постоянной вязкости уравнения движения в общепринятых обозначениях примут вид

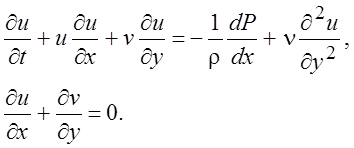                                          (4.15)

Уравнения (4.15) впервые были выведены  Прандтлем (Prandtl, 1904).

Обозначим продольную скорость вдали от тела через V = V (x, t). Поперечную скорость примем равной нулю. Тогда принимая во внимание, что распределение давления в пограничном слое совпадает с тем, которое было бы на поверхности тела в отсутствие пограничного слоя, получим уравнение

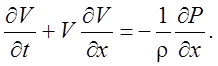                                                    (4.16)

Уравнение (4.16) задает скорость на внешней границе пограничного слоя. В стационарном случае его решением будет интеграл Бернулли

                                        

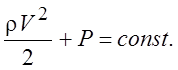
Тогда первое из уравнений Прандтля (4.15) для стационарного течения можно записать в виде

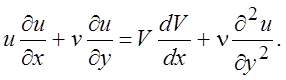                                    (4.17)

Граничные условия требуют обращения в нуль скорости на стенке и асимптотического приближения к скорости невозмущенного потока V(x,t) при удалении от нее.

4.3.  Интегральные характеристики пограничного слоя

Обсудим еще раз те преимущества, которые дает использование уравнений пограничного слоя. С математической точки зрения они существенно проще уравнений Навье-Стокса, но все еще сложны для решения, так как остаются нелинейными уравнениями. Отметим, что уравнения Навье-Стокса являются уравнениями эллиптического типа, в то время как уравнения Прандтля принадлежат к параболическому типу. Допущения, положенные в основу вывода  уравнений пограничного слоя, привели к тому, что давление можно считать постоянным поперек его толщины и определять из решения невязких  уравнений. Оценки показали, что толщина пограничного слоя мала и в первом приближении для расчета внешнего течения ее можно не учитывать.

В качестве характеристики расстояния, на которое невозмущенный поток оттесняется наружу от тела из-за  торможения газа в пограничном слое за счет вязкости, вводят так называемую толщину вытеснения   согласно определению

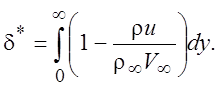                                         (4.18)

Здесь индексом “¥“ отмечены величины, взятые из решения невязкой задачи. Расход идеального газа через поперечное  сечение толщиной d^* равен потере расхода из-за торможения газа в пограничном слое, т.е. из-за торможения газа в пограничном слое линия тока внешнего течения оттесняется на величину d^*. Фактически невязкий поток тело, толщина которого увеличена на d^*. Это обстоятельство позволяет вычислить следующее приближение для расчета пограничного слоя. Расчет невязкого течения во втором приближении ведется для тела, толщина которого увеличена на величину d^*, полученную в первом приближении. Затем снова рассчитывается пограничный слой. Толщина вытеснения представляет собой некоторую меру толщины пограничного слоя более определенную, чем сама толщина d. Обычно за d принимают значение ординаты, для которой продольная скорость в данном сечении отличается на 1% от скорости невозмущенного течения, что вносит некоторую неопределенность.