Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 14

4.1.  Уравнения пограничного слоя

Следуя Прандтлю, разделим течение газа на две области. Первая – очень тонкий пограничный слой в непосредственной близости к поверхности обтекаемого тела, в котором существенны силы вязкости. Вторая – все остальное течение, где вязкость несущественна. Будем считать, что течение во второй области нам известно. Выведем уравнения, описывающие движение газа в первой области.

Обратимся к безразмерной форме записи уравнений движения вязкого газа (1.45). Оценим отдельные члены, входящие в эти уравнения. Для упрощения записи опустим штрихи в обозначении безразмерных переменных. Примем для простоты, что характерные масштабы скорости и расстояния u и L » 1. В направлении x₁ и x₃ на расстояниях » L - характерного размера тела, скорость меняется медленно. Поэтому можно принять, что

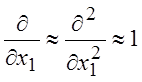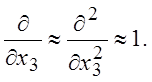  и                                     (4.1)

Для компонент скорости, плотности и давления примем следующие оценки:

                                        (4.2)

Ввиду тонкости пограничного слоя ясно, что течение в нем будет происходить в основном параллельно обтекаемой поверхности. Скорость, направленная по нормали к поверхности u₂, будет мала по сравнению с продольной u₁ и трансверсальной u₃ скоростями. Мы не рассматриваем резких ускорений и будем  считать, что производные по времени одного порядка с инерционными конвективными членами, т.е.

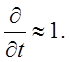                                                    (4.3)

Тогда вывод о малости  нормальной скорости следует непосредственно из уравнения  неразрывности. Если толщина динамического пограничного слоя d << L, то из уравнения неразрывности получим

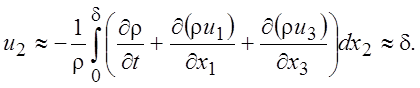                       (4.4)

Оценка производных по нормальной координате дает

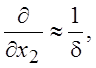
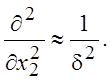                                           (4.5)

Рассмотрим уравнения движения для i = 1 и 3. Подставим в них оценки (4.1) – (4.5). Нетрудно видеть, что с учетом принятых предложений, все инерционные члены (левые части уравнений) одного порядка (~ 1). В правых частях уравнений члены 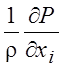 также ~1.

Рассмотрим теперь члены в правой части уравнений, определяемые вязкостью. Так как пограничный слой формируется под действием сил вязкости, то хотя бы один из вязких членов уравнения движения должен быть одного порядка с инерционными членами. Оценки показывают, что таким членом будет

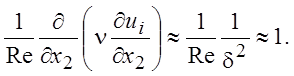                              (4.6)

Остальные вязкие члены ~ 1/Re и ими можно пренебречь.

Для i = 1, 3 получим следующие уравнения:

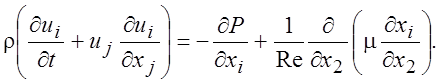                         (4.7)

Соотношение (4.6) дает оценку для безразмерной толщины пограничного слоя: . Если число Рейнольдса достаточно велико, так что d мало, то внешнее потенциальное обтекание будет только слегка нарушаться и в первом приближении для расчета внешнего течения можно считать, что пограничный слой отсутствует.

Рассмотрим теперь второе уравнение движения (i = 2). Подставим в него оценки (4.1) – (4.5) и учтем соотношение  (4.6). Получим, что . Тогда разность давления на стенке и в потоке 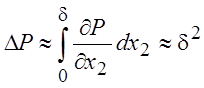 и в рассматриваемом приближении можно просто положить

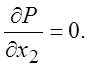                                                 (4.8)

Из вышесказанного следует, что давление в пограничном слое равно давлению в основном потоке газа и может быть получено из решения невязкой задачи.

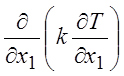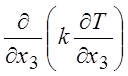Произведем теперь аналогичную оценку для членов уравнения энергии (1.35). Пусть d_T - безразмерная толщина температурного пограничного слоя, малая по сравнению с характерными размерами тела одного порядка с d. Из оценок для членов, зависящих  от конвекции и трения, видно, что членами  и  можно пренебречь по сравнению с 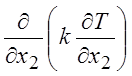. Перенос тепла вследствие теплопроводности будет одного порядка с переносом тепла из-за конвекции только в том случае, если выполняется соотношение

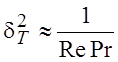,                                                       (4.9)

что непосредственно следует из оценки члена 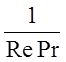 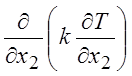в уравнении (1.35). Cвязав это соотношение с (4.6) для толщины динамического пограничного слоя, получим

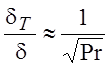.                                                        (4.10)