т.е., если 
не очень велико, выражение (3.18) будет
малой величиной. В силу того, что зазор мал можно считать, что v << u. Оценим
вторые производные в уравнении Навье-Стокса
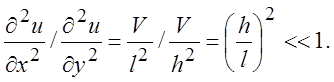(3.19)
В результате из уравнений движения останется только уравнение
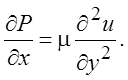(3.20)
Уравнение неразрывности запишем в интегральной форме
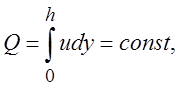(3.21)
где Q - количество жидкости, протекающее в единицу времени через поперечное сечение щели.
Граничные условия имеют вид
при 
при 
(3.22)
при 
Мы приняли, что давления в начале и в конце ползуна совпадают.
Интегрирование (3.20) по y дает
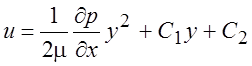. (3.23)
С1 и С2 – константы интегрирования. Используя два граничных условия на скорость (3.22) получаем
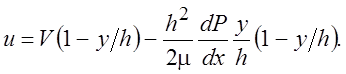(3.24)
Градиент давления является функцией координаты x и его надо определить. Из (3.21) и (3.24) находим
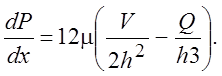(3.25)
Интегрируя выражения (3.25) по х получаем
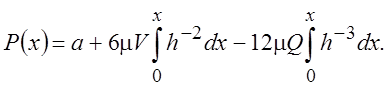(3.26)
Константы 
и Q находим из
граничных условий (3.22) для давления:
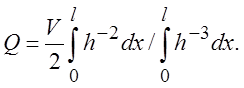(3.27)
Таким образом, если задано уравнение для зазора между ползуном
и опорой и скорость движения опоры, то из (3.27) можно найти количество протекающей
жидкости Q и тем самым из (3.26) – распределение
давления. Зная распределение давления, можно вычислить силы, действующие на
ползун.
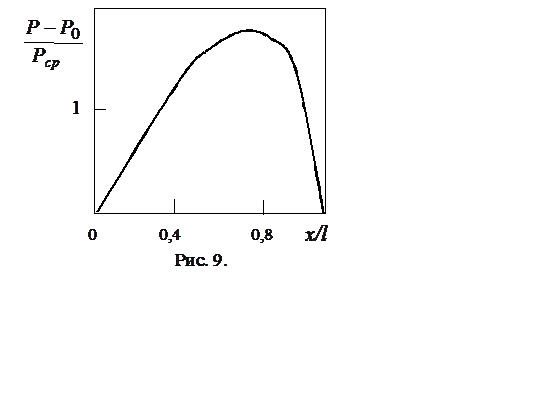
Пример течения в щели между ползуном и опорой дан на рис. 8, а распределение нормированного на среднее значение давления в зазоре – на рис. 9. Видно, что около неподвижной поверхности возникает возвратное течение. Оценка среднего давления под ползуном показывает, что оно » (l/h)2 и может достигнуть очень больших величин.
Задача 3.1.
Облако мелкодисперсных частиц радиусом R равномерно опускается на землю. Оценить скорость снижения облака в зависимости от числа Рейнольдса Re.
Задача 3.2.
Найти положение максимума давления на опору в клиновидном зазоре (рис.8), если его высота определяется соотношением h(x) = d(a-x).
Задача 3.3.
Две параллельные, круглые пластинки радиуса R расположены одна над другой на малом расстоянии h друг от друга и пространство между ними заполнено жидкостью. Пластинки сближаются со скоростью u, вытесняя жидкость. Найти силу сопротивления сближению пластинок.
4. ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ
В данном разделе мы будем рассматривать течения, формирующиеся при больших значениях числа Рейнольдса. Большие числа Рейнольдса эквивалентны очень малой вязкости, и газ можно рассматривать как идеальный. Однако такое приближение непригодно для описания течения газа вблизи твердых поверхностей. Граничные условия для идеальной жидкости требуют обращения в нуль на поверхности только нормальной составляющей скорости. Для вязких реальных газов на поверхности должна обращаться в нуль и продольная составляющая. Для того чтобы выполнить это условие, Прандтль предложил в пределах тонкого пограничного слоя газа, примыкающего к телу, считать, что скорость изменяется от нуля на поверхности до скорости невозмущенного обтекания идеальным газом. Падение скорости в пограничном слое обусловлено вязкостью газа, которой нельзя пренебречь, несмотря на большие значения числа Рейнольдса. В этом слое происходит интенсивное вихревое движение и вязкие силы соизмеримы по величине с инерционными. Математически это проявляется в том, что из-за больших градиентов скорости в тонком пограничном слое вязкие члены в уравнениях движения, содержащие производные скорости по координатам, велики, несмотря на малость m.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.