Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 12

Выражение (3.14) справедливо для Re < 1. Шар медленно движется около наблюдателя со скоростью V , увлекая за собой жидкость. Ширина зоны влияния шара с каждой стороны » D.

Естественно попытаться построить решение для более простого двумерного случая – обтекания цилиндра. Существуют строгие доказательства того, что, оставаясь в рамках приближения Стокса, такое решение построить нельзя. В этом парадокс Стокса. Даже при малых числах Рейнольдса в плоской задаче обтекания нельзя полностью отбрасывать инерционные члены.

3.2. Обтекание шара. Приближение Озеена

Полученное в предыдущем параграфе решение оказывается несправедливым на достаточно больших расстояниях от шара. Отброшенные в уравнениях Навье-Стокса инерционные члены порядка » V²/r. Оставленные в уравнениях вязкие члены » mV/rr². Условие

                                                             

выполняется только на расстояниях

                                                                                                            (3.15)

Таким образом, хотя составляющие скорости стремятся на бесконечности к своим истинным значениям, их распределения на больших расстояниях неправильны и их производные задаются плохо. Сопротивление же шара, вычисленное по формуле Стокса (3.14), дает хорошее приближение, так как определяется для малых значений r .

Для получения решений на больших расстояниях необходимо учесть инерционные члены. Проведем линеаризацию уравнений движения относительно возмущений равномерного  потока, внесенных присутствием шара (C.W. Oseen, 1910). Пусть на бесконечности составляющие скорости V_j = (V, 0, 0). В окрестности шара компоненты скорости можно представить в виде

                                                                                                        (3.16)

Поправки  будем считать малыми величинами относительно . Подставляя (3.16) в уравнения (1.20) и пренебрегая квадратичными членами, получим следующую систему уравнений:

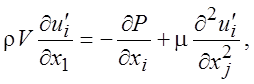                                                                                       (3.15)

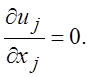                                                 (3.16)

Граничные условия остаются прежними. Из вида уравнений видно, что при смене знака скоростей они уже не переходят сами в себя (из-за члена слева) и описывают уже другое течение.

Решение уравнений (3.15), (3.16) дает

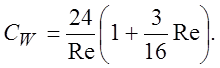 (3.17)

Линии тока и распределение скорости по Озеену для наблюдателя, находящегося далеко от движущегося находящегося далеко от движущегося шара, показаны на рис.7. Картина линий тока не одинакова спереди и сзади тела. Жидкость вытесняется во все стороны. За шаром линии тока группируются плотнее, что указывает на формирование следа. Коэффициент сопротивления, рассчитанный по формуле (3.17), совпадает с экспериментальными данными до Re < 5.

3.3. Течение в слое смазки

Примером течения с преобладающим действием вязкости, важным для технических приложений, является течение смазочного масла в зазоре между движущимися частями машин. Течение вязкого масла в узком зазоре между 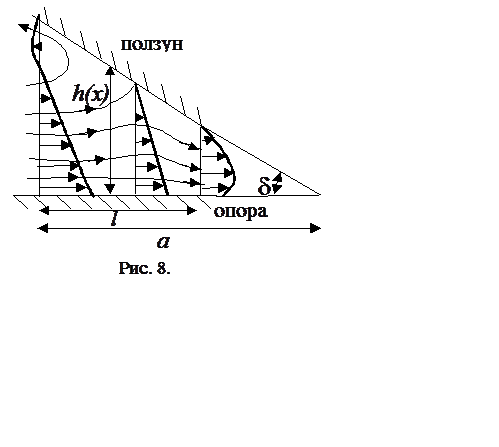цапфой и подшипником обладает следующим свойством. Возникающая в зазоре разность давлений может стать настолько большой, что результирующая сила будет поддерживать цапфу, и она не будет соприкасаться с подшипником. Наиболее существенные особенности течения в узком зазоре можно рассмотреть на простом примере ползуна и плоской опоры.

Рассмотрим две плоскости, образующие между собой малый угол d (рис.8). Верхняя плоскость (ползун) – неподвижна, нижняя (опора) – движется со скоростью V в направлении оси ox. В направлении z опора и ползун имеют очень большое протяжение. В направлении y между ползуном и опорой  образуется тонкая клинообразная щель шириной h(x). Будем считать, что h << l, где l - длина ползуна. Рассмотрим отношение сил – инерции к силам вязкости. Из членов, зависящих от вязкости, наиболее  существенный , тогда

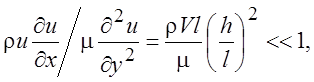                                                                               (3.18)