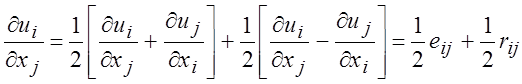Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 5

,                     (1.13)

здесь e_ij - тензор скоростей деформаций; r_ij - тензор, определяющий завихренность движения. Иллюстрация воздействий на элементарный кубический объем двух типов тензорных сил приведена на рис. 2а,б на примере его двумерной проекции. Показаны силы и конечные изменения объема. Видно, что симметричная часть тензора (рис.2,а, справа) вызывает деформацию объема (рис. 2,а слева), а несимметричная часть тнензора (рис. 2,б, слева) вращение объема, как показано на рис. 2,б, справа.

Будем считать, что в однородной среде вязкие напряжения вызываются деформациями, а не вихрями, что характерно для ламинарных течений. Связь между вязкими напряжениями и деформациями дает закон Стокса:

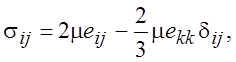                                                 (1.14)

где m - независящий от скорости коэффициент динамической вязкости, а  - символ Кронекера.

                                        0 при i ¹ j

                                          1 при i = j

Выражение (1.14) – эмпирический закон, который требует экспериментальной проверки. В правую часть выражения (1.14) входят два члена, первый из которых определяет вязкие поверхностные силы трения, второй – силы внутреннего трения, возникающие при сжатии.

Тогда силы, вызванные вязкостью и действующие на элементарный объем газа, можно записать в виде

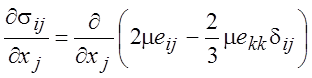.                                    (1.15)

Выражение (1.12) и (1.15) можно объединить, если ввести тензор напряжений

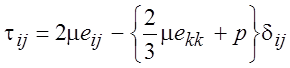.                                        (1.16)

Тогда поверхностные силы можно представить в виде

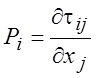.                                                          (1.17)

Уравнение (1.8) теперь можно записать следующим образом:

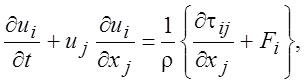 где                       (1.18)

Дифференциальные уравнения (1.18) составляют основу всей аэрогидродинамики и называются уравнениями  Навье-Стокса. Еще раз отметим, что уравнение (1.18) отражает баланс пяти сил: 1) инерционных; 2) сил давления; 3) массовых сил; 4) вязких сил трения; 5) вязких сил сжатия.

От массовых сил в некоторых случаях можно избавиться. Пусть на элемент газа действует только сила тяжести F_k = - rg, совпадающая с направлением координаты x_к. Представим эту силу тяжести в виде вектора . Тогда силовые члены в уравнении (1.18), не связанные с вязкостью, можно преобразовать следующим образом

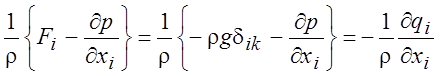,                             (1.19)

где q_i=p+rgx_кd_ik – эффективное давление в жидкости. В таком представлении массовые силы выпадают из уравнений. Подобное упрощение полезно при рассмотрении движения однородной жидкости без свободных границ. Вместо действительного давления рассматривается разность давления при движении и при состоянии покоя (если есть свободные границы, то давление войдет в граничные условия и упрощения не будет).

В данном курсе мы не будем рассматривать примеры с наличием массовых сил. Тогда уравнение (1.18) упростится и будет иметь вид:

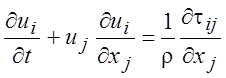.                                                 (1.20)

1.3.  Уравнение энергии

Уравнение энергии для сжимаемой среды выведем из первого начала термодинамики соответствующее закону сохранения энергии в механике. В некотором объеме газа V₀ выполняется баланс подводимого к нему тепла dQ, повышения его полной энергии dE и совершаемой им работы dA:

.                                                   (1.21)

В свою очередь полная энергия объема газа dE состоит из внутренней энергии rC_vdT и кинетической энергии dE_к. Тогда

.                                    (1.22)

В уравнении (1.22) C_v - удельная теплоемкость при постоянном объеме. Будем считать, что она не зависит от температуры. Тогда изменение тепла в объем V₀ за единицу времени должно подчиняться соотношению

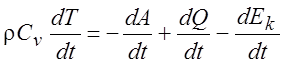.                                       (1.23)

В объем газа тепло может подводиться за счет теплопроводности. Если градиент температуры не слишком велик, можно разложить тепловой поток q в ряд по степеням градиента температуры и ограничиться первым членом разложения (закон Фурье)