Динамика вязкого газа, турбулентность и струи: Учебное пособие, страница 10

Граничные условия: u = 0 при r = R, где R - радиус трубы, скорость ограничена при r = 0. По аналогии со случаем, рассмотренным в параграфе 2.1, получаем p = p(z) и 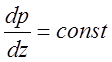. Проинтегрировав (2.23), находим

                                        

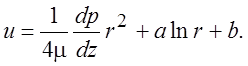
Постоянную a надо положить равной нулю, так как скорость в центре трубы должна оставаться конечной. Постоянную b определяем из граничных условий. Тогда

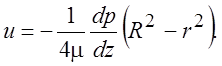.                                        (2.24)

Мы получили параболическое распределение с максимумом на оси трубы при r = 0, 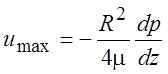 и средним значением скорости, равным .

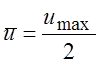Легко определить расход жидкости в трубе

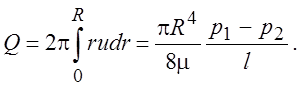                             (2.25)

здесь учтено, что если известно давление на концах трубы длиной l, то 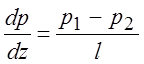. Подставим выражение для средней скорости в (2.25). Тогда расход жидкости в трубе

                                              (2.26)

Введем коэффициент сопротивления l, который подчиняется соотношению

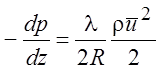                                       (2.27)

и является коэффициентом пропорциональности между падением давления в трубе и скоростным напором. Для рассматриваемого течения

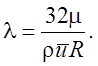                                               (2.28)

Определим число Рейнольдса , вычисленное по диаметру трубы d: 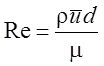. Выражение для l тогда можно представить в виде

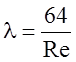.                                                  (2.29)

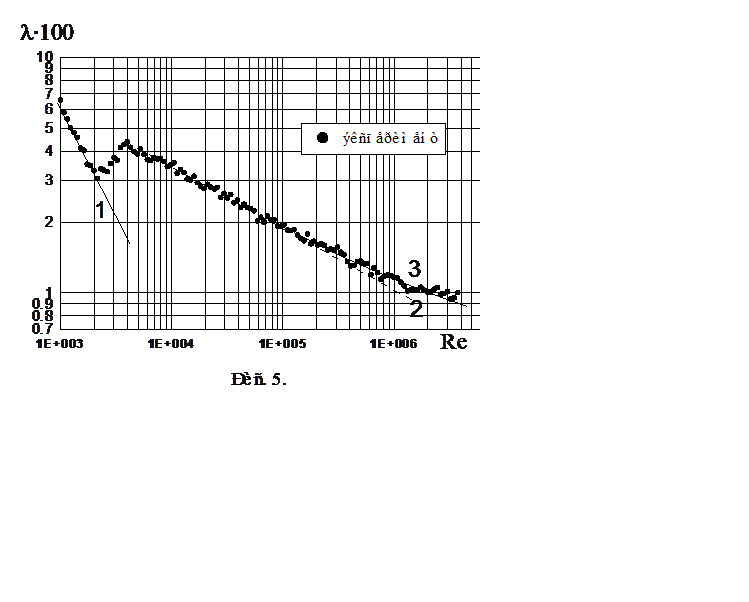
Выражение (2.29) представляет собой закон сопротивления для гладких труб.

2.4.  Несколько замечаний о применимости полученных результатов

Хотя при решении рассмотренных задач не накладывалось никаких математических ограничений на число Рейнольдса, полученные результаты справедливы не всегда. Уравнения Навье-Стокса справедливы для ламинарных течений. При достижении некоторого критического значения числа Рейнольдса Re_кр предположение о слоистости течения нарушается, ламинарное течение становится неустойчивым и переходит в турбулентное состояние. На рис. 5 приведена зависимость l = l(Re) - закон сопротивления для гладких труб. Кривая 1 отражает закон Гагена-Пуазейля (2.29) для ламинарного течения, который достаточно хорошо подтверждается экспериментальными данными до Re_кр » 2300. Для больших чисел Рейнольдса экспериментальные точки отклоняются от зависимости (1) на рис. 5 и соответствуют сначала переходному режиму, а затем турбулентному.

Задача 2.1.

Рассматривается течение между двумя пластинами. На нижней пластине укреплен плавающий элемент – аэродинамические весы, измеряющие касательную силу. Пусть R – радиус чувствительного элемента, 2h – расстояние между пластинами, р₁ и р₂ – давление в зазоре в передней и задней точках элемента. Найти силу, которую покажут весы.

Задача 2.2.

Рассматривается течение между двумя неподвижными пластинами с одинаковой температурой Т₀. Течение осуществляется за счет перепада давления 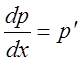. Найти распределение температуры и максимальную температуру в потоке.

Задача 2.3.

Рассмотреть течение в кольцевом зазоре между двумя трубами радиуса R₁ и R₂. Перепад давления Dр на длине трубы l задан. Найти распределение скорости в зазоре.

Задача 2.4.

В вертикальную трубу с внутренним радиусом R, заполненную вязкой жидкостью, вставлен невесомый цилиндр длиной L, радиусом меньшим R на величину h. При этом выполняются следующие неравенства: L>>R и h<<R. Найти стационарную скорость всплывания цилиндра в трубе U.

3.  ПОЛЗУЩИЕ ДВИЖЕНИЯ

При достаточно малых числах Рейнольдса Re < 1 в уравнениях (1.20) можно пренебречь инерционными членами. Тогда стационарное течение несжимаемой жидкости будет описываться следующей системой уравнений:

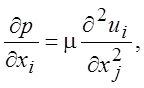
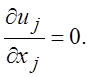                                        (3.1)

Граничные условия остаются прежними. Эти уравнения выполняются для течений, которые характеризуются малыми значениями скорости, большими значениями вязкости или малыми характерными размерами. Уравнения движения в этих случаях становятся линейными и в некоторых случаях для них можно найти точные решения. Полученные решения можно рассматривать как первое приближение решений уравнений Навье-Стокса при малых значениях числа Рейнольдса.