Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане

Содержание ч.2
5.	Анализ волновых движений в океане
		Введение
	5.1	Постановка задачи
	5.2	Анализ простейших случаев
	5.3	Волны Россби
	5.4	Общая схема классификации свободных волн в океане
	5.5	Экваториальные волны Кельвина
	5.6	Захват волн вертикальными стенками. Береговые волны  Кельвина
6.	Уравнения геофизической гидродинамики с учетом турбулентности
	6.1	Осреднение уравнений. Уравнения Рейнольдса
	6.2	Анализ безразмерных параметров
	6.3	Геострофическое приближение
7.	Пограничные слои в океане
	7.1	Поверхностный пограничный слой Экмана
	7.2	Западный пограничный слой
		7.2.1	Метод полных потоков Штокмана
		7.2.2	Западный вязкий програничный слой. Задача Стомелла
	7.3	Инерционный пограничный слой. Свободная инерционная мода Фофонова
	7.4	Проблема термоклина
		Список литературы

5. Анализ волновых движений в океане.

Волновые движения играют важнейшую роль в атмосфере и океане, определяя динамику течений, формируя аномалии давления и плотности и формируя горизонтальную и вертикальную структуру метео и гидрофизических полей. Вследствие того что волновые процессы являются достаточно быстрыми по сравнению со средними течениями, они являются основным механизмом передачи информации в сплошной среде. Следует вспомнить такие волны как поверхностные гравитационные волны, в частности,  приливные волны,  разрушительные волны цунами, внутренние гравитационные волны, во многом формирующие вертикальную структуру гидрофизических характеристик  в атмосфере и океане. Существенную роль в формировании погодных условий в  двух средах, играют планетарные волны Россби, и, наконец, нельзя не упомнить экваториальные волны Кельвина и Пуанкаре, ответственные за возникновение такого явления межгодовой климатической изменчивости как Эль-Ниньо.

Волновые процессы в настоящем разделе будем рассматривать относительно линейной модели  динамики океана, рассматриваемой на -плоскости, что позволит существенно упростить выкладки, сохраняя содержательную часть основных выводов. Атмосферные волновые процессы имеют прямые аналоги с результатами, представленными в настоящей главе с некоторыми изменениями, определяемыми спецификой среды. Исключение, возможно, составляют береговые захваченные волны Кельвина, являющиеся характерными для океана вследствие наличия меридиональных границ.

5.1. Постановка задачи.

Рассмотрим линеаризированные уравнения в безграничном по горизонтали океане с постоянной глубиной  на –плоскости в отсутствие вязких членов. В третьем уравнении движения сохраняем эволюционный член.

Уравнения имеют вид:

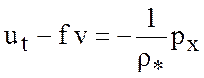,                                            (5.1)

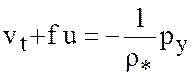,                                              (5.2)

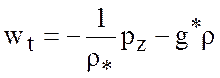,                                          (5.3)

где .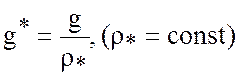

В приближении Буссинеска  имеем

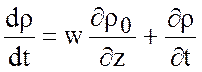
Тогда уравнение притока плотности 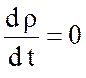 перепишется в виде

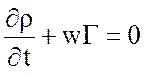,                                               (5.4)

где 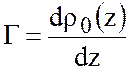 - градиент стандартной плотности по вертикали,

а из уравнения неразрывности

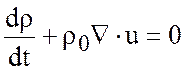
получаем

.

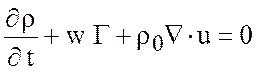Тогда, учитывая (5.4) получим

,                                                      (5.5)

Если (5.3) продифференцировать по  и применить (5.5), то получим

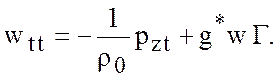                                         (5.6)

Будем рассматривать область ограниченной глубины  с поверхностью , причем . Тогда из разложения

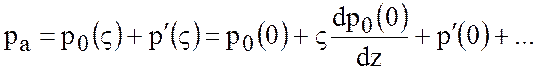                   (5.7)

и уравнения статики 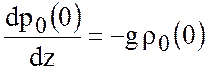, следует линеаризованное динамическое условие

.                                            (5.8)

Линеаризованное кинематическое условие будет иметь вид

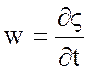,                                                                     (5.9)

На дне  ставится условие непротекания

,                                                          (5.10)

а на поверхности при , объединяя (5.8), (5.9), опуская штрихи и полагая , получаем

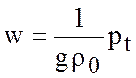.                                                (5.11)

Будем рассматривать периодические во времени волновые движения в безграничном океане. Решение ищем  в виде простой гармоники с частотой .

.

Тогда из (5.1) - (5.3) получим

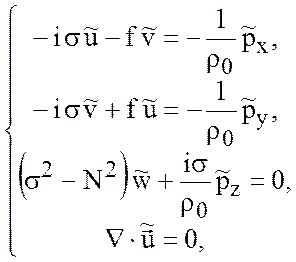                                        (5.12)

где .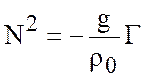

Рассмотрим движение с положительной стратификацией, то есть ,  - вещественное. Структура уравнений (5.12) позволяет искать решение методом разделения переменных.