Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 10

Уравнения геофизической динамики являются сложными трехмерными нелинейными системами  дифференциальных уравнений, разрешаемые только современными численными методами, что осуществляется в настоящее время в современных климатических моделях. Однако, во времена отсутствия ЭВМ анализ уравнений динамики атмосферы и океана проводился на аналитическом уровне, что позволило получить важные качественные результаты, не потерявшие свою ценность и в настоящее время. К таким направлениям качественного исследования уравнений динамики океана относится метод «полных потоков», развивавшийся в нашей стране  известным океанографом В.Б.Штокманом. Этот подход позволил исследовать характерные черты горизонтальных движений планетарной жидкости на примере океана, абстрагируясь от термических и бароклинных процессов. Следствием этого подхода являются результаты последующих разделов 7.2.2, 7.3. Рассмотрим уравнения динамики океана

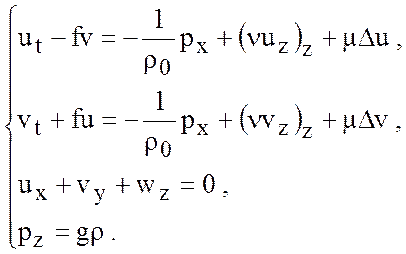                        (7.17)

Считаем, что  (океан - баротропный).. Проинтегрируем уравнение статики  от  до , при граничных условиях для давления на поверхности при  : . Получим

.

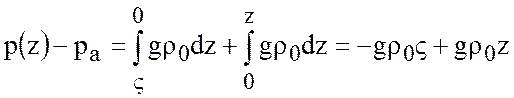Отсюда, при

,

учитывая, что , получаем

.

После этого, считая отклонение о возмущенного уровня малыми, граничные условия на поверхности можно перенести на уровень :

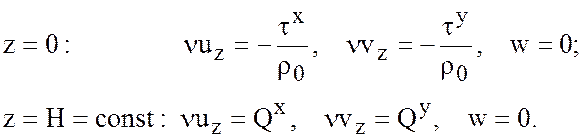
Здесь  - вектор-функция трения о дно. Проинтегрируем далее систему (7.17) в пределах от 0 до .

Обозначая проинтегрированные во глубине скорости, называемые «полными потоками»

,

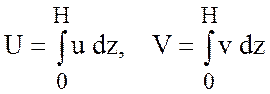приходим к выражениям

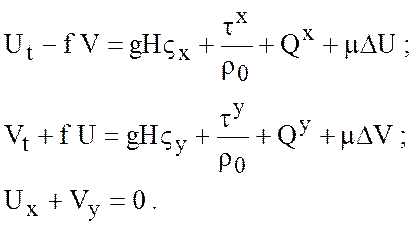                       (7.18)

Введем конкретный вид вектора в виде линейного «ньютоновского»  закона трения о дно

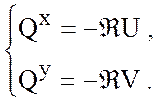
Иногда в моделях циркуляции вместо полных потоков удобно использовать средние по вертикали значения вектора скорости. Обозначая

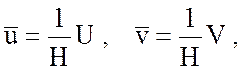
перепишем (7.18) в виде

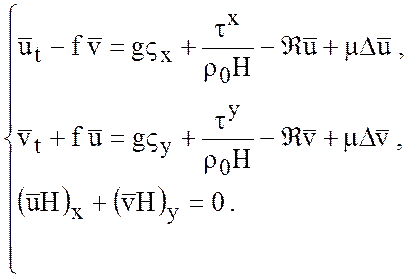                        (7.19)

Применим к первым двум уравнениям операцию вихря. Продифференцируем первое уравнение системы (7.19) по , второе - по  и вычтем из второго уравнения первое с использованием соотношений

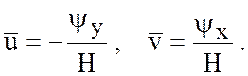
В результате получим уравнение для вертикальной компоненты относительного вихря в терминах интегральной функции тока

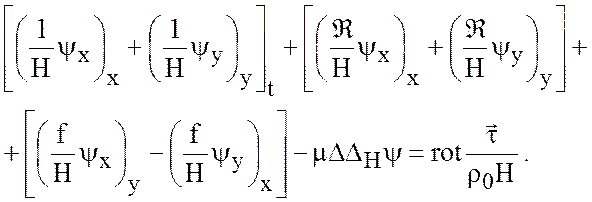           (7.20)

Здесь .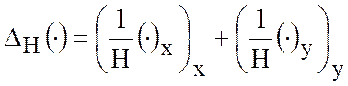

Если убрать источники и стоки, то это уравнение будет иметь свободные решения, в виде волн Россби.

Уравнение (7.20) можно записать в терминах вихря. Обозначая , где  - вертикальная компонента вихря, уравнение (7.20) перепишется в виде

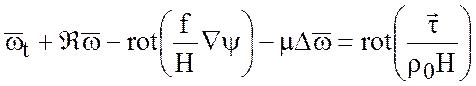.                           (7.21)

В уравнении (7.21) Члены приобретают более наглядный смысл. Первый член определяет величину изменения вихря по времени. Второе слагаемое характеризует диссипацию вихря за счет трения о дно.  Третье слагаемое описывает -эффект при  и при  равняется . Четвертое слагаемое – сток энергии вихря за счет турбулентной вязкости. Слагаемое в правой части – источник движения за счет действия касательного напряжения трения ветра.

Из уравнения вихря можно получить весьма полезное для качественного анализа «соотношение Свердрупа», отбросив в (7.21) малые слагаемые:

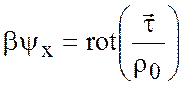,                                               (7.22)

,

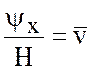,                                                      (7.23)

.

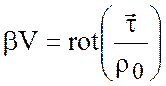Соотношение Свердрупа позволяет сделать важные оценки. Если океан имеет восточную меридиональную границу при , , тогда полагаем

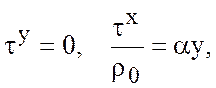
то есть

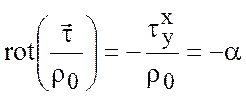.                                              (7.24)

Уравнение (7.23) принимает вид

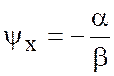
или

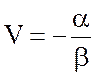,                                                      (7.25)

то есть течение направлено на юг.

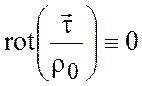Если существует такая широта, что , то  и течение эту широту не пересекает.

Проинтегрируем соотношение Свердрупа от восточной границы  на запад:

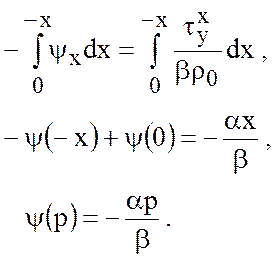
Здесь мы ввели обозначения . Кроме того, поскольку граница  является линией тока можно положить  . Интегральная функция тока имеет физический смысл расхода  воды между восточной границей и точкой в средней части океана. Этот факт является замечательным следствием соотношения Свердрупа, поскольку для того, чтобы рассчитать количество воды, которое проходит между восточным и западным меридианами в океане достаточно  знать распределение ветра над океаном. Этот прием на первых этапах развития теории динамики океана часто использовался для расчета интегральных переносов водных масс в океанах.