для фиксированной широты ![]() . Из (6.14) следует, что сила Кориолиса
уравновешивается градиентом давления, а из (6.17) - что уравнение притока тепла
свелось к уравнению сохранения температуры на траектории.
. Из (6.14) следует, что сила Кориолиса
уравновешивается градиентом давления, а из (6.17) - что уравнение притока тепла
свелось к уравнению сохранения температуры на траектории.
Уравнения (6.14) - (6.17) называются геострофическим приближением, а выражение
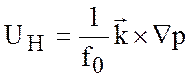
Называют геострофической скоростью. Или покомпонентно
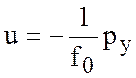 , (6.18)
, (6.18)
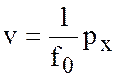 . (6.19)
. (6.19)
Таким образом, давление является функцией тока, а скорость касательна к изолиниям давления.
Заметим, что геострофическое движение бездивергентно. В самом деле,
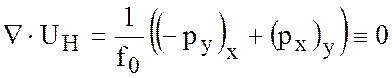 .
.
тогда из (6.16) следует, что 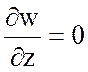 , то есть, если в геострофическом движении
, то есть, если в геострофическом движении ![]() на некотором уровне
на некотором уровне ![]() , то
, то ![]() для
любого
для
любого ![]() .
.
Дифференцируя уравнения (6.18),
(6.19) по ![]() и используя соотношение между давлением и
температурой
и используя соотношение между давлением и
температурой ![]() , получим
, получим
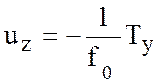 , (6.20)
, (6.20)
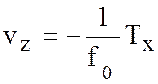 . (6.21)
. (6.21)
(6.20) - (6.21) - соотношения термического ветра для геострофического приближения.
Система уравнений (6.14) - (6.17) является вырожденной. Геострофическое приближение, приводя к очень простым и изящным выражениям, представляет собой лишь диагностическое соотношение. Информация, содержащаяся в геострофических соотношениях, недостаточна для полного определения динамики движения. Поэтому нужно решать общую систему, не отбрасывая малые члены или выделять отдельно каждый из пограничных слоев и рассматривать их физический смысл на аналитических решениях. Исследование каждого из пограничных слоев будет представлено далее.
7. Пограничные слои в океане.
7.1. Поверхностный пограничный слой Экмана.
Вертикальное турбулентное трение играет важную роль в геофизической гидродинамике, являясь механизмом, формирующим вертикальную структуру метео-гидрофизических полей вблизи горизонтальных границ атмосферы и океана и осуществляющим влияние даже на глубинные зоны океана посредством результирующих вертикальных движений.
Рассмотрим случай чисто дрейфового течения в океане, вызванного ветром постоянной силы и постоянного направления. В этом случае мы находимся в поверхностном слое океана в пределах выделенного нами в предыдущем разделе пограничного слоя Экмана [7], названного так по имени шведского геофизика, сумевшего выделить основные механизмы формирования поверхностного ветрового дрейфового слоя и решившего эту задачу о повороте поверхностного ветрового течения по отношению к направлению ветра. Впервые эффект отклонения дрейфа льдов от направления ветра наблюдал Ф.Нансен во время дрейфа судна «Фрам» в Арктике. Аналогичный пограничный слой существует в атмосфере, реализующий систему вязких течений у поверхности Земли.
Итак, в пределах пограничного слоя доминирующими силами являются сила Кориолиса и сила вертикальной турбулентной вязкости. Градиенты давления вследствие безграничности океана и постоянства ветра являются нулевыми, В рамках этих масштабов предполагаем, что плотность воды постоянна. При этом условии нелинейные члены в уравнениях движения пренебрежимо малы с точностью до числа Россби. В уравнениях оставляем только эволюционные члены, чтобы впоследствии рассмотреть развитие дрейфовых течений во времени.
В результате уравнения движения принимают форму
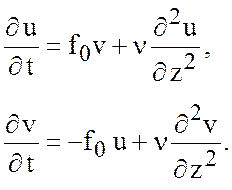 (7.1)
(7.1)
В случае установившегося движения левые части в уравнениях (7.1) обращаются в нуль. Тогда введя сокращенное обозначение
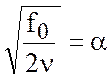
нетрудно из (7.1) получить уравнения движения жидкости в виде
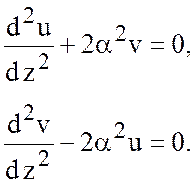 (7.2)
(7.2)
Общий интеграл этих уравнений имеет вид
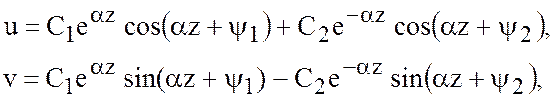 (7.3)
(7.3)
где ![]() и
и ![]() - константы интегрирования, определяемые
на основании граничных условий.
- константы интегрирования, определяемые
на основании граничных условий.
Проще всего задача решается в
случае бесконечной глубины. В дальнейшем будет показано, что практически те же решения
реализуются при конечных глубинах. Итак, пусть глубина моря бесконечно
велика. Тогда при условии конечных скоростей течения необходимо, чтобы члены
уравнений (7.3), содержащие ![]() , отсутствовали (
, отсутствовали (![]() ).
).![]() и
и ![]() определяются, продифференцировав по
определяются, продифференцировав по ![]() уравнения (7.3), переписанные в виде
уравнения (7.3), переписанные в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.