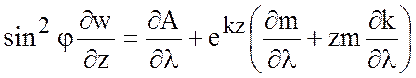Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 15

.                                    (7.65)

Интегрируя это уравнение по , и используя, что   на поверхности океана  при , находим

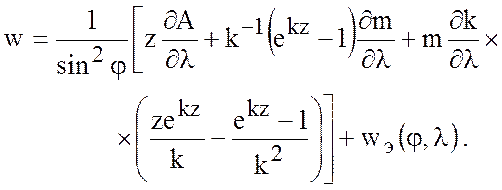                               (7.66)

Подставляя (7.64) и (7.66) в (7.55), получаем после несложных преобразований

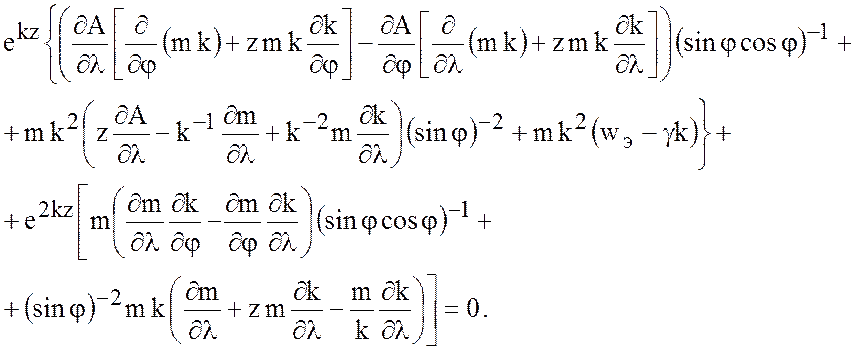              (7.67)

Для того чтобы (7.64) действительно было решением, все коэффициенты при различных функциях переменной  в (7.67) должны по отдельности обращаться в нуль. Это означает, что каждый из коэффициентов перед функциями  должен обращаться в нуль. Рассмотрим сначала коэффициент при . Он равен нулю, когда

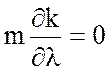.                                                    (7.68)

Если , т.е. бароклинное поле не равно тождественно нулю, то  не зависит от долготы. Таким образом, . Коэффициент при  также должен быть нулем, откуда с учетом (7.68) следует

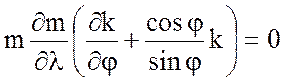.                                         (7.69)

Аналогично обращение в нуль коэффициентов при  дает соответственно

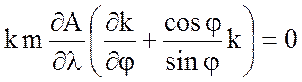,                                      (7.70)

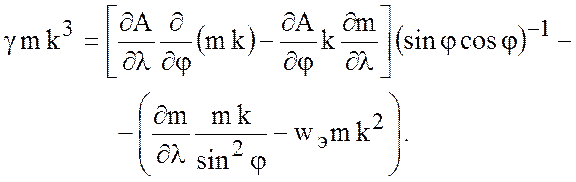              (7.71)

 Для выполнения условий (7.69) и (7.70) необходимо, чтобы либо  и  одновременно не зависели от , либо

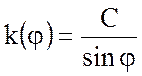 ,                                              (7.72)

где  - произвольная константа. В первом случае поле давления не зависит от долготы и  в точности равно нулю. Это в свою очередь означает, что  для всех . Тогда у дна океана должен тогда образовываться экмановский пограничный слой, компенсирующий эту вертикальную скорость. Чтобы такой экмановский слой существовал, необходима большая (порядка 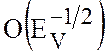) зональная скорость во внутренней области. Однако если  равно , то это невозможно, и таким образом, должно выполняться (7.72). Отсюда в свою очередь следует, что вертикальный масштаб для термоклина дается формулой

,

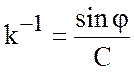согласно которой глубина термоклина уменьшается при приближении к экватору, что качественно согласуется с наблюдениями. Если  не равно нулю, то  содержит слагаемое, линейно зависящее от . В баротропном океане именно такое слагаемое создает растяжение вихревых трубок, приводящее к возникновению меридионального движения. В случае стратифицированного океана, когда ищется решение для  , асимптотически стремящееся к фиксированному значению при , мы должны выбрать  не зависящее от , что приводит к чисто зональной баротропной скорости. Если на больших глубинах зональная скорость обращается в нуль на меридиональной (скажем, на восточной) границе, то  само должно равняться нулю для всех  и . Мы ограничимся поэтому чисто бароклинным решением, т.е. положим . Из условия (7.62) при  получаем

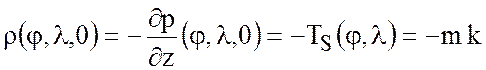 ,                         (7.73)

откуда находим функцию :

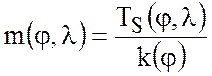.                                                   (7.74)

Таким образом, решение уравнений теории термоклина имеет вид

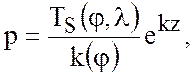
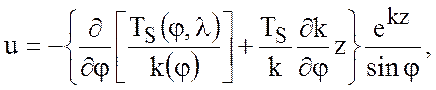                    (7.75)

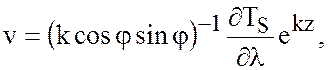
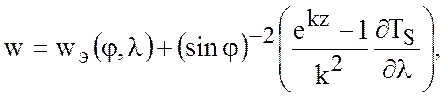
при условии, что

,

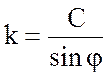где  - произвольная положительная константа в силу (7.71)

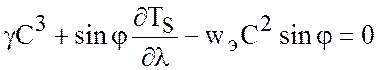.                           (7.76)

Из последней формулы (7.75) следует, что при  скорость  стремится к асимптотическому значению

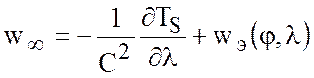,                                    (7.77)

которое с учетом (7.76) можно записать как

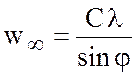.                                                (7.78)

Поскольку

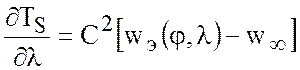                                       (7.79)

и  полностью определяется заданием , построенное решение жестко связывает  и . Фактически (7.79) есть не что иное, как соотношение Свердрупа, так как интегрирование по вертикали уравнения (7.52) дает

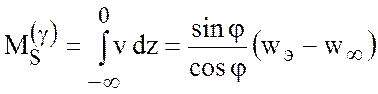,                            (7.80)

откуда с учетом четвертого соотношения (7.75) следует (7.77). Поскольку меридиональная скорость прямо пропорциональна , соотношение Свердрупа ограничивает возможные распределения вертикальной скорости на нижней границе экмановского слоя так, чтобы  было совместно с заданным градиентом по  температуры на поверхности. Произвольно может задаваться только одна из функций  и , другая при этом находится по соотношению Свердрупа. Искусственная связь между  и  возникает исключительно из-за предположения об автомодельной формы решения.