Рис. 5.6.
Дисперсионное соотношение для волн этого типа имеет вид:
![]() .
.
Чтобы волна уменьшилась в ![]() раз в направлении
раз в направлении ![]() ,
надо пройти расстояние
,
надо пройти расстояние 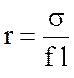 ,
, 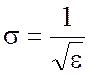 . Дисперсионное соотношение для этих волн
. Дисперсионное соотношение для этих волн
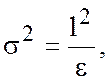
поэтому иногда константу разделения
выбирают в виде ![]() , которая имеет смысл фазовой
скорости, здесь
, которая имеет смысл фазовой
скорости, здесь ![]() - характерная глубина процесса. Тогда
- характерная глубина процесса. Тогда
![]() , если
, если ![]() -
полная глубина океана.
-
полная глубина океана. 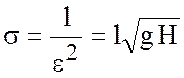 , следовательно,
, следовательно, ![]() км (для
км (для ![]() км на
широте
км на
широте ![]() . Эти волны играют роль в прибрежной
динамике).
. Эти волны играют роль в прибрежной
динамике).
6. Уравнения геофизической гидродинамики с учетом турбулентности.
6.1. Осреднение уравнений. Уравнения Рейнольдса.
В предыдущих лекциях мы
описывали получение уравнений при использовании в уравнениях молекулярной
кинематической вязкости. Однако, на масштабах, изучаемых нами, влияние этих
коэффициентов на крупномасштабные течения пренебрежимо мало. Для океана
коэффициенты кинематической вязкости имеют значение ![]() и для
атмосферы
и для
атмосферы ![]() .
.
С одной стороны, очевидно, что другого механизма диссипации, кроме молекулярной вязкости не существует, с другой стороны, понятно, что мы никогда не сможем в крупномасштабных моделях описать всю цепочку вихревых образований и турбулентных движений, которые передают энергию от крупномасштабных движений к мелкомасштабным и затем - в тепло. Это соответствует понятию каскадной передачи энергии, то есть крупномасштабные течения не существуют изолированно. Должен существовать целый спектр разномасштабных движений, поддерживаемых за счет энергии крупномасштабных движений. В отдельных районах и в отдельные периоды могут существовать процессы передачи энергии от мелких масштабов к крупным, однако, в целом эта концепция является оправданной. Тогда может быть сделана попытка описать динамику передачи энергии от крупных масштабов к мелким только через кинематические свойства самого крупномасштабного движения. В ином случае мы должны решать невообразимую по сложности задачу по описанию всех масштабов в одной системе уравнений.
На самом деле проблема удовлетворительного описания взаимодействия мелко- и крупномасштабных движений является одной из самых трудных и неясных в геофизической гидродинамике. В настоящее время не существует такой теории турбулентности, которая бы давала не очень сложное, но достаточно адекватное описание эффективной силы трения, обусловленной каскадной передачей энергии турбулентными и вихревыми флуктуациями.
В настоящем разделе кратко дано описание простейшей параметризации влияния каскада турбулентных движений на крупномасштабные движения, полностью аналогичные описанию молекулярных сил на средние движения в уравнениях Навье-Стокса. Необходимо понимать, что описываемая параметризация является вынужденным компромиссом Озмидов [8 ].
Рассмотрим уравнения системы (4.12), (4.11) с учетом вязкости
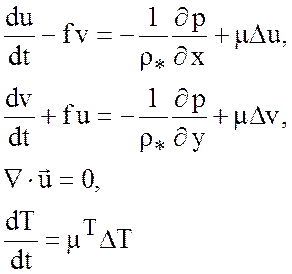 (6.1)
(6.1)
![]() ,
,
Где использованы стандартные обозначения
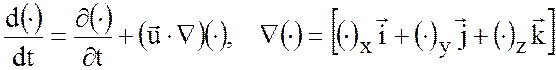 .
.
Для разделения
гидродинамических полей на крупномасштабную и турбулентную составляющие
применяется операция пространственно-временного осреднения полей. Движения
осредняются по ![]() ,
, ![]() следующим
образом. Полагается, каждая функция представима в виде
следующим
образом. Полагается, каждая функция представима в виде
![]() ,
,
где ![]() и
и ![]() - средняя составляющая и пульсация,
соответственно. Операция осреднения
- средняя составляющая и пульсация,
соответственно. Операция осреднения ![]() удовлетворяет следующим
правилам Рейнольдса
удовлетворяет следующим
правилам Рейнольдса
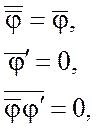
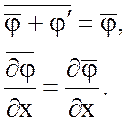
В терминах теории вероятности, ![]() может трактоваться как математическое
ожидание, а
может трактоваться как математическое
ожидание, а ![]() - как дисперсия. Тогда первое из уравнений
движения (6.1) может быть переписаны в виде
- как дисперсия. Тогда первое из уравнений
движения (6.1) может быть переписаны в виде
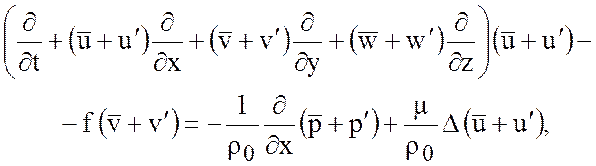
где ![]() -
молекулярная вязкость. Осредняя правую и левую части уравнения, получаем
-
молекулярная вязкость. Осредняя правую и левую части уравнения, получаем
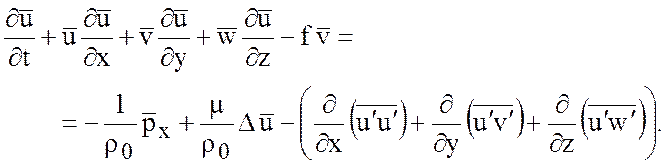 (6.2)
(6.2)
Здесь для дивергентного представления
адвективных членов для отклонений использовано уравнение неразрывности ![]() . Помножая его на
. Помножая его на ![]() ,
получим
,
получим
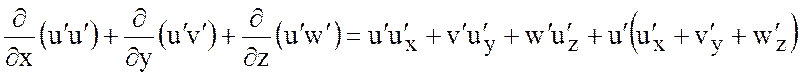 .
.
Аналогично выводятся уравнения
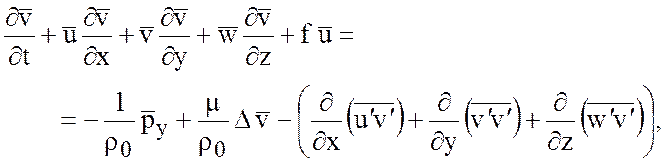 (6.3)
(6.3)
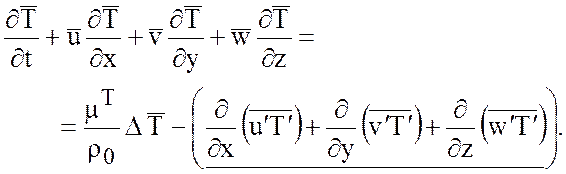 (6.4)
(6.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.