Подчеркнутые члены отвечают за
турбулентные потоки импульса и тепла. Можно строить бесконечную цепочку
уравнений для моментов, но где-то эту цепочку нужно обрывать. Поэтому решили
выразить осредненные потоки через среднее движение. Таким образом, потоки
импульса и тепла, обусловленного мелкомасштабным движением, похожи на потоки
импульса и тепла, полученные при изучении членов молекулярной вязкости. Вопрос,
который является чрезвычайно сложным, состоит в следующем: как определить эти
напряжения и потоки тепла? Можно построить уравнения относительно этих
моментов, комбинируя уравнения для ![]() ,
, ![]() ,
, ![]() ,
, ![]() и осредняя их. Получаются уравнения для
нахождения
и осредняя их. Получаются уравнения для
нахождения ![]() ,
, ![]() ,
, ![]() ,
, ![]() и так
далее. Но в правых частях этих уравнений уже будут стоять третьи моменты вида
и так
далее. Но в правых частях этих уравнений уже будут стоять третьи моменты вида ![]() . Получается бесконечная последовательность
уравнений для моментов все более высокого порядка, которые в случае
исследования общей циркуляции атмосферы и океана реализовать невозможно.
. Получается бесконечная последовательность
уравнений для моментов все более высокого порядка, которые в случае
исследования общей циркуляции атмосферы и океана реализовать невозможно.
Простейшее и наименее обоснованное замыкание для определения турбулентных потоков импульса и тепла через средние величины будем проводить, используя гипотезы называемые гипотезами Ричардсона.
Обозначим
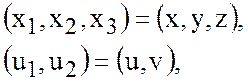
![]() - единичные орты осей координат.
- единичные орты осей координат.
Гипотезы замыкания имеют вид:
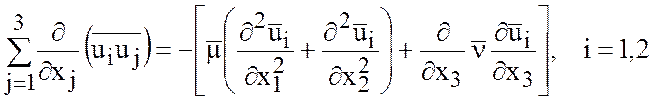
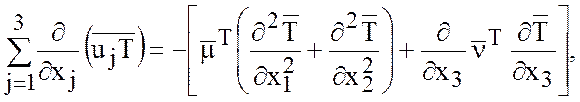
где ![]() -
горизонтальная турбулентная вязкость,
-
горизонтальная турбулентная вязкость, ![]() -
вертикальная турбулентная вязкость,
-
вертикальная турбулентная вязкость, ![]() ,
, ![]() - соответствующие коэффициенту диффузии в
уравнении притока тепла.
- соответствующие коэффициенту диффузии в
уравнении притока тепла.
Тогда, пренебрегая членами с молекулярной вязкостью и диффузией, уравнения принимают следующий вид
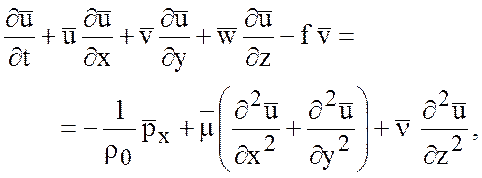
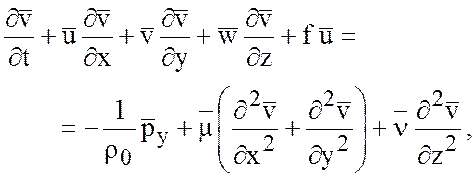 (6.5)
(6.5)
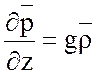
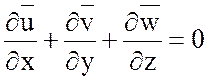
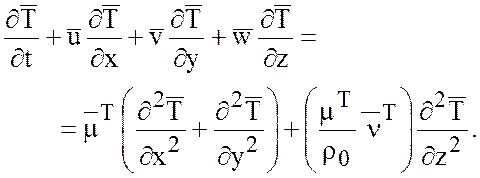
Доказать справедливость этих гипотез на основе физических рассуждений невозможно. Это весьма грубые приближения, однако, в глобальных моделях они используются из-за простоты и удобства реализации. Характерные значения турбулентной вязкости и теплопроводности в океане оцениваются следующим образом (Озмидов [8])
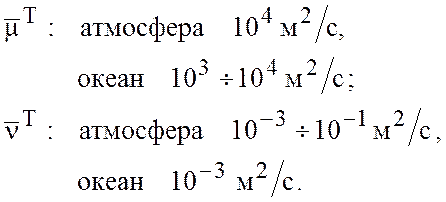
6.2. Анализ безразмерных параметров.
Обозначим ![]() . Используя введенные гипотезы и опуская в
дальнейшем все черты над величинами, записываем уравнения (6.5) в следующем
виде
. Используя введенные гипотезы и опуская в
дальнейшем все черты над величинами, записываем уравнения (6.5) в следующем
виде
|
|
(6.6) (6.7) (6.8) (6.9) |
где ![]() ,
,
![]() - коэффициент термического расширения,
- коэффициент термического расширения, ![]() ,
, ![]() -
вертикальный орт.
-
вертикальный орт.
Введем безразмерные переменные
![]()
![]()
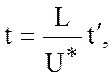
![]()
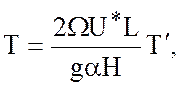
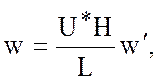
![]()
и безразмерные числа
·
число Россби: 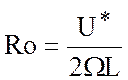 , (описывает вклад в уравнения членов:
ускорение/Кориолис),
, (описывает вклад в уравнения членов:
ускорение/Кориолис),
·
числа Экмана: 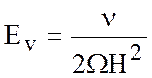 - вертикальное,
- вертикальное, 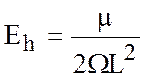 -
горизонтальное, (описывают вклад в уравнения членов: турбулентная
вязкость/Кориолис),
-
горизонтальное, (описывают вклад в уравнения членов: турбулентная
вязкость/Кориолис),
·
числа Пекле: 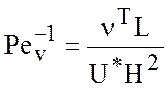 - вертикальное,
- вертикальное, 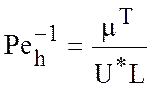 -
горизонтальное (описывают вклад в уравнения притока тепла турбулентной
диффузии),
-
горизонтальное (описывают вклад в уравнения притока тепла турбулентной
диффузии),
здесь ![]() -
угловая скорость вращения Земли,
-
угловая скорость вращения Земли, ![]() - характерная скорость
движения,
- характерная скорость
движения, ![]() - горизонтальный масштаб,
- горизонтальный масштаб, ![]() - вертикальный масштаб. Считаем, что
- вертикальный масштаб. Считаем, что ![]() ,
, ![]() .
Умножив уравнение (6.6) на
.
Умножив уравнение (6.6) на 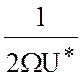 , а уравнение (6.9) на
, а уравнение (6.9) на ![]() , получим систему уравнений в безразмерных переменных.
Штрихи в дальнейшем опускаем. Таким образом, уравнения принимают вид
, получим систему уравнений в безразмерных переменных.
Штрихи в дальнейшем опускаем. Таким образом, уравнения принимают вид
![]() , (6.10)
, (6.10)
![]() , (6.11)
, (6.11)
![]() , (6.12)
, (6.12)
![]() , (6.13)
, (6.13)
здесь ![]() .
Покажем, что безразмерные числа
.
Покажем, что безразмерные числа ![]() ,
, ![]() ,
, ![]() ,
, 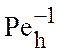 ,
, ![]() являются
малыми величинами.
являются
малыми величинами.
Рассмотрим характерные значения для океана
![]()
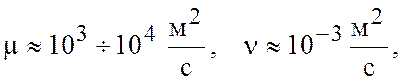
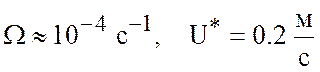 - в центре океана.
- в центре океана.
При таких значениях характерных величин
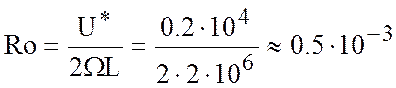 ,
,
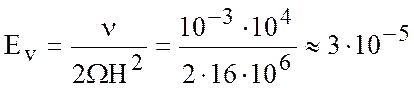 ,
,
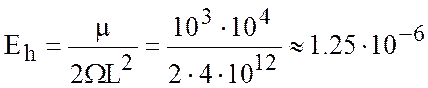 ,
,
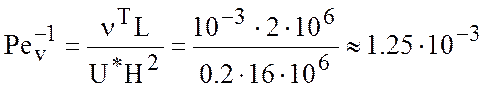 ,
,
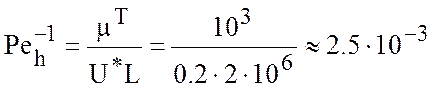 .
.
Малые параметры имеют следующий физический смысл (см. рис. 6.7)
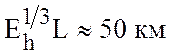 -
толщина бокового вязного пограничного слоя трения,
-
толщина бокового вязного пограничного слоя трения,
![]() - толщина
инерционного пограничного слоя (невязкий слой),
- толщина
инерционного пограничного слоя (невязкий слой),
![]() -
толщина экмановского пограничного слоя,
-
толщина экмановского пограничного слоя,
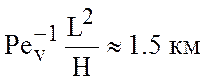 -
глубина термоклина (термическое взаимодействие атмосферы и океана),
-
глубина термоклина (термическое взаимодействие атмосферы и океана),
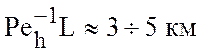 -
боковой пограничный слой диффузии плотности.
-
боковой пограничный слой диффузии плотности.
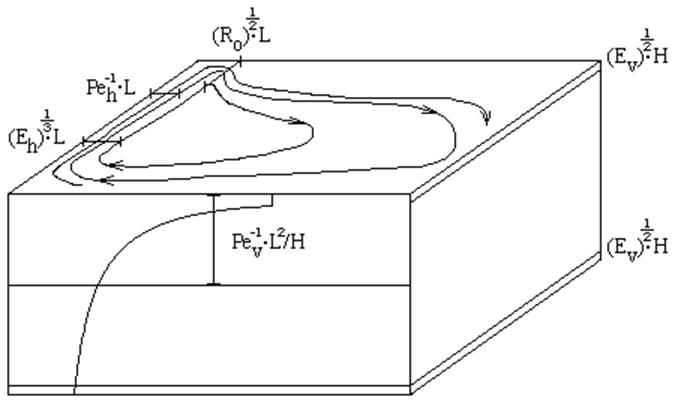
Рис. 6.7.
6.3. Геострофическое приближение
Если в уравнениях (6.10) - (6.13) отбросить все малые члены, то получим следующую систему уравнений
![]() , (6.14)
, (6.14)
![]() , (6.15)
, (6.15)
![]() , (6.16)
, (6.16)
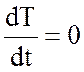 , (6.17)
, (6.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.