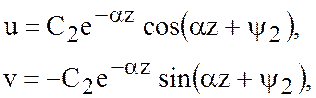Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 8

                                     (7.4)

тогда

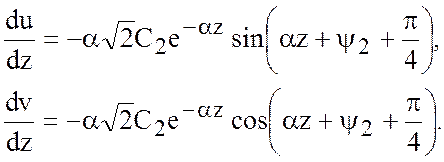                   (7.5)

Считаем, что  скорость ветра направлена по оси , тогда с  с этой осью должна совпадать сила , вызывающая дрейфовое течение. Для потока импульса не поверхности должны выполняться граничные условия

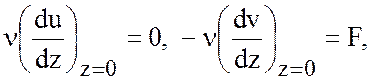
Откуда после подстановки производных из (7.5) получаем

.

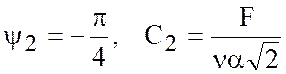Из (7.4) вытекает, что на поверхности моря при ,

,

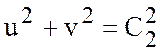т.е. константа  представляет собой абсолютную величину скорости поверхностного течения, которую обозначим .

В результате (7.4) перепишется в виде

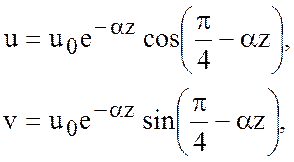                                        (7.6)

где

.

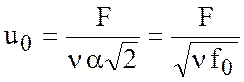Итак, абсолютная величина скорости дрейфового течения на поверхности моря  пропорциональна тангенциальной силе трения, возникающей при движении воздуха над поверхностью воды, а ее направление составляет угол  с направлением ветра, причем течение отклоняется вправо от ветра в северном полушарии. В южном полушарии отклонение происходит в левую сторону от направления ветра.

При увеличении  абсолютная величина вектора скорости течения экспоненциально уменьшается, а его направление поворачивается вправо.

Из формулы (7.6) вытекает, что  при  вектор скорости оказывается направленным в сторону, противоположную направлению скорости поверхностного течения.

Обозначим эту величину

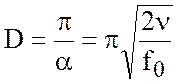.                                          (7.7)

Глубина  зависит от коэффициента турбулентной вязкости . Поэтому  называется глубиной трения (или глубиной "действия трения").

При  вектор скорости совпадает по направлению с вектором поверхностной скорости . Ниже глубины трения скорости течения ничтожно малы. Так при :  ; при : .

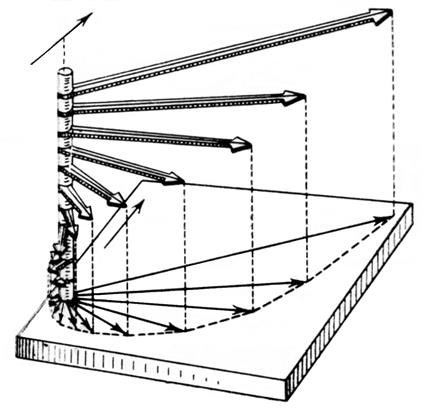
Рис. 7.8. Годограф скорости с глубиной.

На рис. 7.8 изображен годограф скорости с глубиной. Стрелками обозначены скорости на глубинах, меняющихся через промежуток, равный  от глубины трения . Наибольший вектор, отклоненный на  от направления вектора от оси , представляет собой скорость поверхностного течения. Годографом векторов служит логарифмическая спираль, быстро приближающаяся к полюсу.

Из рисунка видно, что вектор, представляющий скорость на глубине , т.е. на половине глубины трения, перпендикулярен к вектору . Векторы, лежащие выше него, дают некоторую слагающую в направлении поверхностного течения . Векторы же, лежащие между ним и глубиной , дают слагающие, направленные в противоположную сторону. Следовательно, можно констатировать, что в слое толщиной  возникает течение, направленное согласно с : это - течение поверхностного слоя. Под ним непосредственно лежит слой глубинного течения, направленного в общей сложности в противоположную сторону.

Вычислим полные потоки воды во всей толще, охваченной дрейфовым течением. Пусть поток в направлении оси  (перпендикулярно к ветру) будет , а в направлении оси  (по направлению ветра) - . Тогда, интегрируя выражения  и  по всей толще воды, найдем

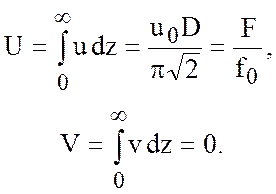                                           (7.8)

Таким образом, результирующий поток  направлен перпендикулярно к силе , действующей на поверхности воды ().

Коэффициент турбулентной вязкости  - величина изменчивая. Иногда коэффициент трения оценивается через глубину трения . Из (7.7)

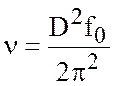.                                                   (7.9)

В случае конечной глубины  константы интегрирования  и  должны быть такими, чтобы при  обе составляющие скорости  и  обращались в нуль. Для определения этих констант удобнее сделать замену переменных - положить . Новая переменная  выражает собой высоту исследуемой точки над дном моря. Из условий на дне вытекает, что константы  и  равны между собой. Обозначим каждую из них через . Также можно показать, что константы  и  отличаются только знаками, а потому их можно заменить через  и . Тогда уравнения (7.3) примут вид

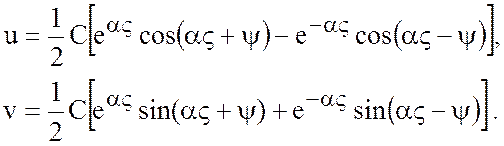                        (7.10)

Можно  переписать (7.10) с помощью гиперболических функций:

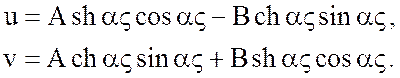                         (7.11)

Константы  и  выражаются следующим образом:

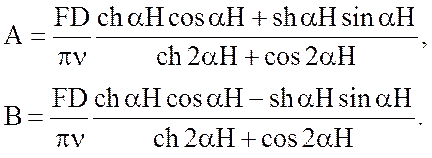                     (7.12)