Ширина этого погранслоя ![]() , а скорость течения
, а скорость течения 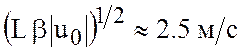 . Взаимодействие западного вязкого
пограничного слоя с инерционным слоем дает различные картины рециркуляции и может
быть проведено на основе численных расчетов.
. Взаимодействие западного вязкого
пограничного слоя с инерционным слоем дает различные картины рециркуляции и может
быть проведено на основе численных расчетов.
7.4. Проблема термоклина.
Термическое взаимодействие атмосферы и океана является ключевым вопросом геофизической гидродинамики и теории климата. Атмосфера, являясь сильно нелинейной динамической системой, «забывает» начальное состояние за период порядка двух недель. «Память» океана в зависимости от масштабов движений составляет периоды от месяцев до тысяч лет. Вертикальное квазистационарное термическое состояние океана характеризуется наличием планетарного пограничного слоя так называемого «термоклина», полученного при оценке безразмерных параметров в разделе 6.2. Термин «планетарность» означает, что горизонтальные масштабы уже сравнимы с радиусом Земли.
В этом случае, когда
горизонтальный масштаб движений становится очень большим так, что ![]() , тогда уравнения квазигеострофического
движения не могут быть записаны в приближении
, тогда уравнения квазигеострофического
движения не могут быть записаны в приближении ![]() -плоскости,
и это приводит к квазигеострофическим соотношениям в сферических координатах, в
которых пренебрегается всеми членами трения и адвекции в уравнениях движения, но
сохраняются нелинейные члены в уравнении притока плотности. Эти уравнения уже
являются более содержательными, чем уравнения на
-плоскости,
и это приводит к квазигеострофическим соотношениям в сферических координатах, в
которых пренебрегается всеми членами трения и адвекции в уравнениях движения, но
сохраняются нелинейные члены в уравнении притока плотности. Эти уравнения уже
являются более содержательными, чем уравнения на ![]() - и на
- и на ![]() -плоскости. Оценки характерных величин для
этого случая можно найти в книге Педлоски [6]. Для этой системы уравнений введем
безразмерные величины в следующем виде (физические величины обозначены индексом
*)
-плоскости. Оценки характерных величин для
этого случая можно найти в книге Педлоски [6]. Для этой системы уравнений введем
безразмерные величины в следующем виде (физические величины обозначены индексом
*)
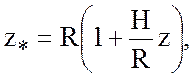
![]()
![]()
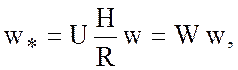
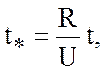
![]()
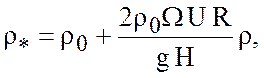
где R – радиус
Земли, ![]() - угловая скорость вращения Земли,
- угловая скорость вращения Земли, ![]() - вертикальный масштаб, U – характерная горизонтальная скорость,
- вертикальный масштаб, U – характерная горизонтальная скорость, ![]() -
величина, описывающая полное изменение плотности в пространстве и времени без
учета приближения Буссинеска,
-
величина, описывающая полное изменение плотности в пространстве и времени без
учета приближения Буссинеска, ![]()
![]() -
давление,
-
давление, ![]() - ускорение свободного падения соответственно.
Окончательно, в безразмерном виде уравнения примут вид
- ускорение свободного падения соответственно.
Окончательно, в безразмерном виде уравнения примут вид
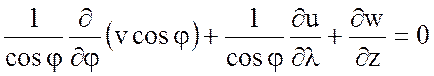 , (7.47)
, (7.47)
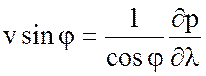 , (7.48)
, (7.48)
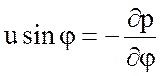 , (7.49)
, (7.49)
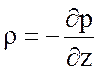 , (7.50)
, (7.50)
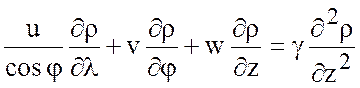 . (7.51)
. (7.51)
Здесь уравнения выписаны в
безразмерном виде и оставлены только метрические коэффициенты. ![]() представляет собой параметризацию
вертикального турбулентного обмена
представляет собой параметризацию
вертикального турбулентного обмена
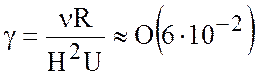 ,
,
где ![]() ,
, ![]() ,
, ![]() . Уравнения
(7.47) - (7.51) уже не являются вырожденными и обладают нетривиальными
решениями.
. Уравнения
(7.47) - (7.51) уже не являются вырожденными и обладают нетривиальными
решениями.
Исключаем давление из уравнений движения
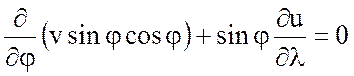
или
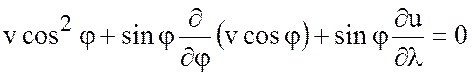 .
.
Используя уравнение неразрывности (7.47), получаем
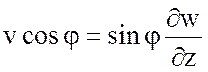 . (7.52)
. (7.52)
В размерном виде соотношение (7.52) имеет вид
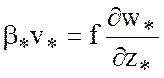 , (7.53)
, (7.53)
где 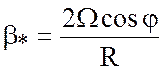 ,
, ![]() . С
учетом (7.48) из (7.52) получаем
. С
учетом (7.48) из (7.52) получаем
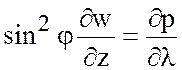 . (7.54)
. (7.54)
Уравнение для плотности (7.51) в стационарном случае с использованием геострофических соотношений (7.48), (7.49) и гидростатики (7.50) сводится к виду
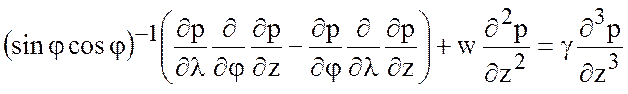 . (7.55)
. (7.55)
Граничные условия для этой системы следующие. На верхней границе геострофической области, описываемой уравнениями (7.54), (7.55) должна задаваться вертикальная скорость. Это означает, что описываемая здесь динамика справедлива ниже верхнего экмановского слоя. Вертикальная скорость в размерных единицах дается формулой (т.н. «экмановская подкачка»), вычисляемой из решения уравнений Экмана
 . (7.56)
. (7.56)
Итак, ![]() на
верхней границе определяется касательным напряжением ветра. Определим экмановскую
вертикальную скорость как
на
верхней границе определяется касательным напряжением ветра. Определим экмановскую
вертикальную скорость как
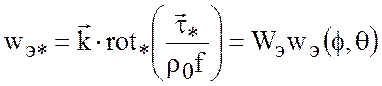 , (7.57)
, (7.57)
где ![]() -
характерная величина
-
характерная величина ![]() . Далее, запишем условие для
. Далее, запишем условие для ![]() при
при ![]() в виде
в виде
![]() (7.58)
(7.58)
или как
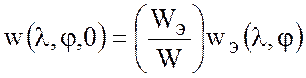 . (7.59)
. (7.59)
Удобно выбрать ![]() равным
равным ![]() , так что из (7.59)
, так что из (7.59)
![]() . (7.60)
. (7.60)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.