|
|
|
Рис.5.5
5.5. Экваториальные волны Кельвина.
Кроме свободно распространяющихся волн в открытом океане существуют еще и волны, связанные с волноводами и береговыми линиями.
На экваторе параметр Кориолиса
равен нулю (![]() ). Экватор является «волноводом», то есть
вдоль него распространяются различные виды так называемых «захваченных» волн, в
частности, экваториальные волны Кельвина, существующие только в окрестности
экватора.
). Экватор является «волноводом», то есть
вдоль него распространяются различные виды так называемых «захваченных» волн, в
частности, экваториальные волны Кельвина, существующие только в окрестности
экватора.
Рассмотрим баротропную жидкость
![]()
В этих обозначениях проинтегрируем уравнения движения и неразрывности (5.1), (5.2), (5.5) по вертикали с граничными условиями
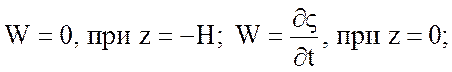
считая ![]() , а
, а ![]() - мало. В результате получаем
линеаризованные уравнения мелкой воды на «бета» - плоскости:
- мало. В результате получаем
линеаризованные уравнения мелкой воды на «бета» - плоскости:
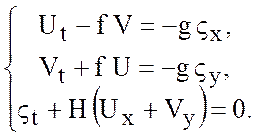 (5.36)
(5.36)
Считая, что волны распространяются вдоль
экватора, полагаем ![]() , тогда первые два уравнения
образуют гиперболическую систему уравнений
, тогда первые два уравнения
образуют гиперболическую систему уравнений
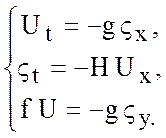 (5.37)
(5.37)
и сводятся к следующему уравнению относительно ![]()
![]() , (5.38)
, (5.38)
где ![]() . Отсюда общее решение ищется в виде
. Отсюда общее решение ищется в виде
![]() .
.
Тогда
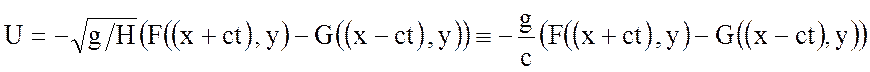 ,
,
подставляя в систему последнее уравнение
(5.37) и учитывая, что ![]() и на экваторе при
и на экваторе при ![]() , т.е.
, т.е. ![]() ,
получим
,
получим
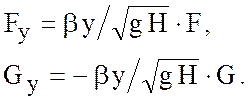
Будем искать те решения,
которые при ![]() ограничены по
ограничены по ![]() . Это
условие требует, чтобы
. Это
условие требует, чтобы ![]() , и решением будет функция
, и решением будет функция ![]()
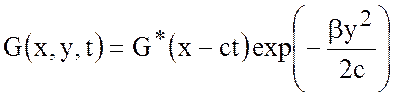 ,
,
где ![]() -
функция, описывающая форму волны. Например, для гармонической волны
-
функция, описывающая форму волны. Например, для гармонической волны ![]() , где
, где ![]() . Таким
образом, волны Кельвина не обладают дисперсией, их фазовая скорость направлена на
восток. Общее решение имеет вид
. Таким
образом, волны Кельвина не обладают дисперсией, их фазовая скорость направлена на
восток. Общее решение имеет вид
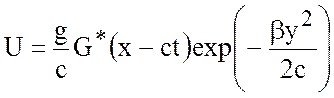 ,
,
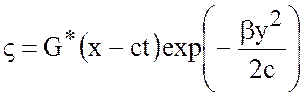 ,
,
![]()
При удалении от экватора волна
уменьшается в ![]() раз на расстоянии
раз на расстоянии 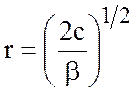 . Если фазовая скорость для баротропных
волн в океане
. Если фазовая скорость для баротропных
волн в океане ![]() м/с, то
м/с, то 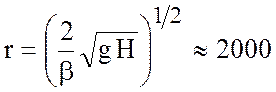 км.
км.
Таким образом, полоса, в которой существенно влияние экваториальных волн может захватывать 4000 км. Это может создать значимые аномалии гидрофизических характеристик в тропической зоне океана, которые могут передаваться атмосферой на далекие расстояния с помощью волнового механизма «дальней связи». Примером может служить формирование волновыми процессами положительных аномалий температуры поверхности океана в восточной части тропиков Тихого океана в период явления Эль-Ниньо. Аналогичные экваториальные захваченные волны присутствуют и в атмосфере, определяя тропическую динамику воздушных течений.
5.6. Захват волн вертикальными стенками. Береговые волны Кельвина.
Следует отметить, что не
только экваториальная зона относится к зонам «волноводов». Океаническая "информация"
также может передаваться вдоль берега с помощью береговых захваченных волн
Кельвина. На ![]() -плоскости рассматриваем
-плоскости рассматриваем ![]() -задачу раздела 5.1
-задачу раздела 5.1
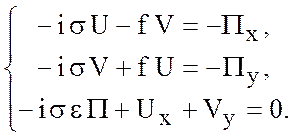 (5.39)
(5.39)
Задачу будем решать в
бассейне, ограниченном вертикальной стенкой при ![]() .
Считаем, что в направлении
.
Считаем, что в направлении ![]() движения нет, полагая
движения нет, полагая ![]() . Тогда уравнения примут вид
. Тогда уравнения примут вид
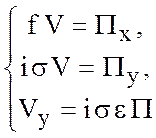 (5.40)
(5.40)
Или, в физическое пространство, перепишем
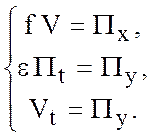 (5.41)
(5.41)
Полагаем, что решение представимо в виде,
допускающем следующее представление ![]() . Тогда решение (5.41) аналогично
предыдущему разделу можно определить в виде
. Тогда решение (5.41) аналогично
предыдущему разделу можно определить в виде
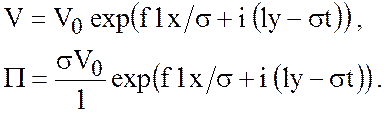
Или, учитывая, что ![]()
![]() ,
,
![]() .
.
![]()
Таким
образом, вдоль границы распространяется волна, которая называется береговой
волной Кельвина. Для того, чтобы она затухала при удалении от стенки, должно
выполняться условие ![]() . Для северного полушария
. Для северного полушария ![]() , откуда следует
, откуда следует ![]() (см.
пояснения к рис. 5.6)
(см.
пояснения к рис. 5.6)
|
|
1. Волна экспоненциально убывает при удалении от стенки. 2. Волна всегда движется так, что стенка остается справа. у западной границы волна движется с севера на юг, у восточной - с юга на север, в южном полушарии - наоборот. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.