Исходная система (7.29), (7.30) может быть записана в виде
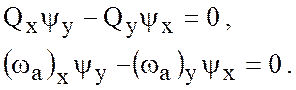 (7.31)
(7.31)
Здесь ![]() ,
, ![]() - функции от
- функции от ![]() ,
, ![]() . Н.П.Фофонов (1958) предложил рассмотреть
линейную зависимость вида
. Н.П.Фофонов (1958) предложил рассмотреть
линейную зависимость вида ![]() . На
. На ![]() -плоскости
-плоскости ![]() -
линейная функция широты, тогда
-
линейная функция широты, тогда
![]() . (7.32)
. (7.32)
Решение ищется в области
![]() .
.
Граничные условия:
![]() .
.
Тогда уравнение (7.32) примет вид
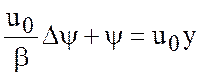 , (7.33)
, (7.33)
где ![]() ,
, ![]() .
.
Введем безразмерные переменные
![]() ,
, ![]() ,
, ![]() . В терминах этих переменных уравнение (7.33)
примет вид
. В терминах этих переменных уравнение (7.33)
примет вид
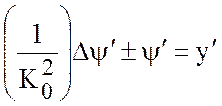 , (7.34)
, (7.34)
где 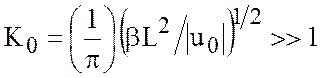 , знак
, знак
![]() соответствует тому, что течение направлено
на запад, а знак
соответствует тому, что течение направлено
на запад, а знак ![]() - на восток.
- на восток.
Граничные условия перепишутся в виде:
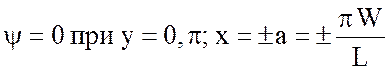 .
.
Будем рассматривать наиболее содержательно
случай когда ![]() (западное течение). Опуская штрихи получим
(западное течение). Опуская штрихи получим
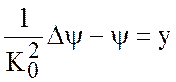 . (7.35)
. (7.35)
Тогда решение уравнения (7.15) ищется в виде:
![]() - частное решение
неоднородного уравнения,
- частное решение
неоднородного уравнения,
![]() - общее решение
однородного,
- общее решение
однородного,
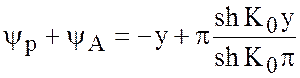 - общее решение неоднородного
уравнения.
- общее решение неоднородного
уравнения.
Нужно теперь ввести
зависимость по ![]() и удовлетворить граничным
условиям. Ищем решение в виде
и удовлетворить граничным
условиям. Ищем решение в виде ![]() , где
, где 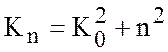 . Путем разложения
. Путем разложения ![]() в
ряд Фурье определяем коэффициенты
в
ряд Фурье определяем коэффициенты ![]() , удовлетворяя граничным
условиям. Общее решение задачи запишется в виде
, удовлетворяя граничным
условиям. Общее решение задачи запишется в виде
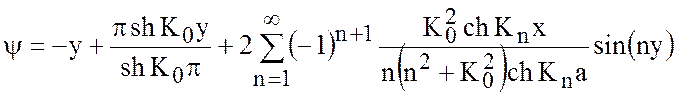 . (7.36)
. (7.36)
Вид решения (7.36) неконструктивен с точки
зрения физического анализа, поскольку содержит малые члены, которые могут быть
отброшены, упрощая выражение. В самом деле, если ![]() ,
, ![]() ,
, ![]() , тогда
, тогда
![]() .
.
Способ нахождения приближенного
решения (7.35) основан на теории пограничных слоев и асимптотических
разложений. На основе наших оценок будем считать, что 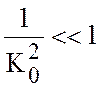 ,
тогда можем осуществлять асимптотическое разложение по малому параметру
,
тогда можем осуществлять асимптотическое разложение по малому параметру 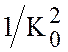 . Итак, рассматриваем уравнение (7.35)
. Итак, рассматриваем уравнение (7.35)
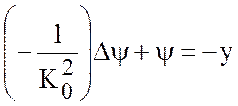 (7.37)
(7.37)
при граничных условиях:
![]()
![]() .
.
Решение будем искать в виде ![]() , где
, где ![]() -
решение редуцированного уравнения
-
решение редуцированного уравнения ![]() , а
, а ![]() - функции, описывающие
пограничные слои. Они нужны для того, чтобы обеспечить выполнение граничных
условий:
- функции, описывающие
пограничные слои. Они нужны для того, чтобы обеспечить выполнение граничных
условий:
![]() .
.
Решения в погранслоях ![]() , ищутся в виде асимптотических разложений
, ищутся в виде асимптотических разложений 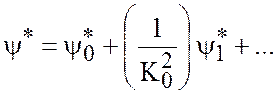 , с сохранением только первых слагаемых. Здесь
, с сохранением только первых слагаемых. Здесь
![]() - общее обозначение для
- общее обозначение для ![]() .
.
Так как вся неоднородность
задачи заключена в решении ![]() , то для нахождения
функций погранслоев будем решать однородные уравнения
, то для нахождения
функций погранслоев будем решать однородные уравнения
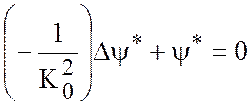 . (7.38)
. (7.38)
1)
Рассматриваем уравнение вблизи границы ![]() . Вводим
в погранслое быструю переменную
. Вводим
в погранслое быструю переменную ![]() ,
, ![]() (она быстро меняется на малом отрезке
(она быстро меняется на малом отрезке ![]() ). Тогда
). Тогда
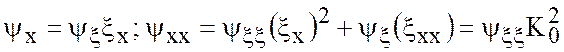 . (7.39)
. (7.39)
Подставляем это в уравнение (7.38)
и приравниваем члены при одинаковых степенях 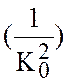 . Для
. Для ![]() получаем уравнение
получаем уравнение
![]() , (7.40)
, (7.40)
при граничных условиях
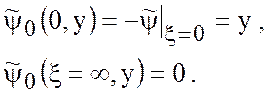
Общее решение имеет вид
![]() ,
,
где константы ![]() и
и ![]() находятся из граничных условий. Тогда
находятся из граничных условий. Тогда ![]() ,
, ![]() . В
результате
. В
результате
![]() . (7.41)
. (7.41)
2)
Найдем решение в окрестности границы ![]() . По аналогии с
вариантом 1) вводим быструю переменную у правой границы
. По аналогии с
вариантом 1) вводим быструю переменную у правой границы ![]() .
Решение ищем в виде асимптотического разложения
.
Решение ищем в виде асимптотического разложения 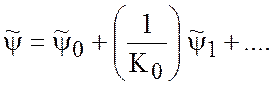 . Тогда
для
. Тогда
для ![]() выполняется уравнение
выполняется уравнение
![]() , (7.42)
, (7.42)
при граничных условиях
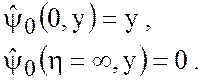
Решение имеет вид
![]() . (7.43)
. (7.43)
Обозначим далее для наглядности
![]() .
.
3)
Осталось рассмотреть вариант с формированием погранслоя у границы ![]() , подбирая
, подбирая ![]() такое,
чтобы
такое,
чтобы ![]() . Вводя переменную
. Вводя переменную ![]() ,
получаем уравнение
,
получаем уравнение
![]() , (7.44)
, (7.44)
с граничными условиями
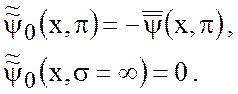
Решение имеет вид
![]() , (7.45)
, (7.45)
где
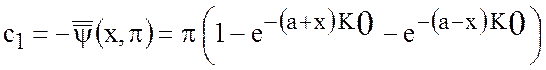 ,
,
![]() .
.
Таким образом, окончательно общее решение имеет вид
![]() . (7.46)
. (7.46)
Оно описывает инерционный пограничный слой у северной границы и дает описание механизма возникновения рециркуляции Гольфстрима (Рис. 7.10).
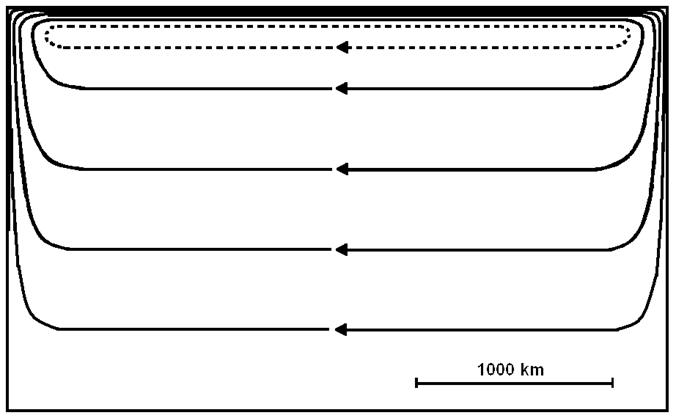
Рис.7.10. Картина свободного инерционного пограничного слоя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.