7.2.2. Западный вязкий пограничный слой. Задача Стомелла.
Особенность соотношений Свердрупа состоит в том, что полученные по ним линии тока, описывающие расход масс не являются замкнутыми и оканчиваются на западной границе океана.
Однако эта сложность достаточно легко разрешается. В идеализированной постановке эта задача была решена Г.Стоммелом в 1948 году. Основная идея состоит в том, что уравнение (7.20) содержит члены трения, способные сформировать у западного берега океана пограничное течение, компенсирующее поток массы на юг в средних широтах и снимающие парадокс соотношения Свердрупа с незамкнутыми изолиниями функции тока и замкнуть их. Возникающее при этом направленное на север пограничное течение является аналогом мощных струйных течений Гольфстрима и Куросио, существующие в западных частях Атлантического и Тихого океана.
Рассмотрим задачу (7.20) в
бассейне прямоугольной формы со сторонами ![]() по
по ![]() и
и ![]() по
по ![]() . Полагая процесс стационарным и
пренебрегая турбулентной вязкостью
. Полагая процесс стационарным и
пренебрегая турбулентной вязкостью ![]() , получим
, получим
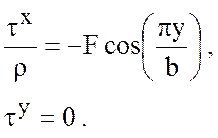
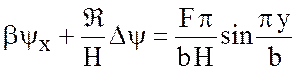 . (7.26)
. (7.26)
Значения параметров выбираем следующими
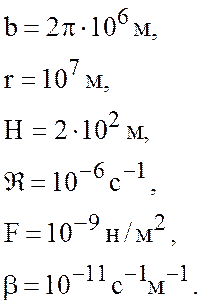
Частное решение (7.17) имеет вид
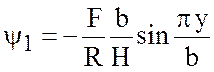 .
.
Общее решение ищем методом разделения переменных:
![]() ,
,
где 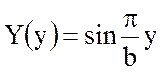 , а
для нахождения
, а
для нахождения ![]() решается характеристическое
уравнение
решается характеристическое
уравнение
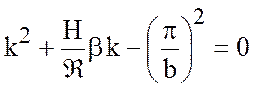
с корнями
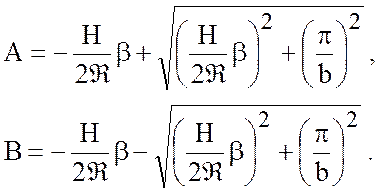
Общее решение запишется в виде
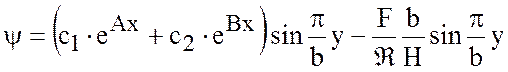 .
.
Находя значения ![]() и
и
![]() из граничных условий
из граничных условий ![]() ,
, ![]() и
подставляя эти значения в формулу общего решения, получим
и
подставляя эти значения в формулу общего решения, получим
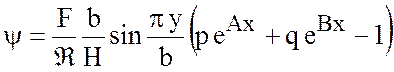 , (7.27)
, (7.27)
где 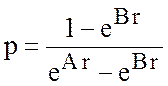 ,
, ![]() .
.
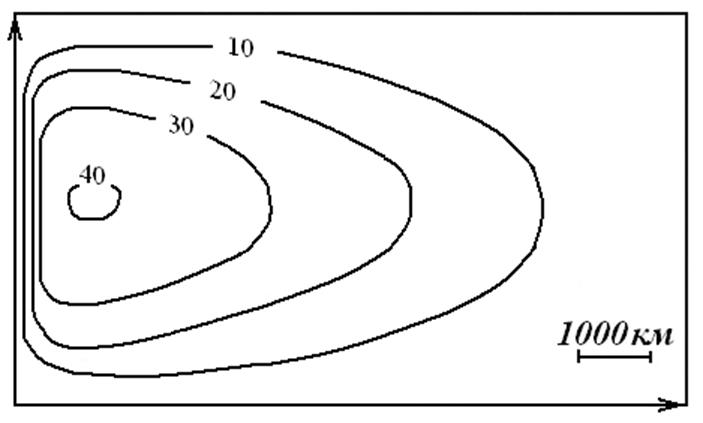
Рис. 7.9. Картина значений функции тока.
Если подставлять в решение (7.27)
численные значения параметров задачи (7.26), получим несимметричную картину по ![]() с пограничным слоем у границы
с пограничным слоем у границы ![]() и распределением в соответствии с
соотношением Свердрупа внутри области. Полученный пограничный слой является
вязким пограничным слоем, но у западного берега возникает он вследствие
и распределением в соответствии с
соотношением Свердрупа внутри области. Полученный пограничный слой является
вязким пограничным слоем, но у западного берега возникает он вследствие ![]() - эффекта. В приближении
- эффекта. В приближении ![]() - плоскости, т.е. когда
- плоскости, т.е. когда ![]() мы получаем абсолютно симметричную картину
относительно линии
мы получаем абсолютно симметричную картину
относительно линии 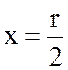 .Этот пограничный слой описывает,
как уже указывалось механизм формирования течений Гольфстрим в Атлантическом
океане и хорошо описывается сложными климатическими моделями динамики океана.
.Этот пограничный слой описывает,
как уже указывалось механизм формирования течений Гольфстрим в Атлантическом
океане и хорошо описывается сложными климатическими моделями динамики океана.
7.3. Инерционный пограничный слой (Свободная инерционная мода Фофонова)
Решение Г. Стоммелом проблемы
формирования Гольфстрима выдвинуло новые вопросы, связанные с поведением
течения Гольфстрим в Атлантике после отрыва от континентального склона
Американского континента на широте ![]() . Измерения,
проведенные в центральной части океана показали парадоксальное поведение
течения на северной периферии субтропического круговорота. Измерениями были
обнаружено направление некоторых южных ветвей Гольфстрима, аномальным образом на
запад. Эти ветви течения
. Измерения,
проведенные в центральной части океана показали парадоксальное поведение
течения на северной периферии субтропического круговорота. Измерениями были
обнаружено направление некоторых южных ветвей Гольфстрима, аномальным образом на
запад. Эти ветви течения ![]() были названы
«рецеркуляцией» Гольфстрима. Анализ, проведенный геофизиком- океанографом Н.П.Фофоновым
в 1954 году показал, что этот эффект является следствием взаимодействия вязкого
западного пограничного слоя и инерционного пограничного слоя, представленных
нами в разделе 6.2. у северной границы субтропического круговорота.
были названы
«рецеркуляцией» Гольфстрима. Анализ, проведенный геофизиком- океанографом Н.П.Фофоновым
в 1954 году показал, что этот эффект является следствием взаимодействия вязкого
западного пограничного слоя и инерционного пограничного слоя, представленных
нами в разделе 6.2. у северной границы субтропического круговорота.
Для выделения эффекта
формирования инерционной моды в течениях рассмотрим простейший случай, когда глубина
постоянна и жидкость баротропна (![]() ,
, ![]() ), и течение предполагается стационарным.
Тогда уравнения движения жидкости, проинтегрированные по вертикали от
поверхности
), и течение предполагается стационарным.
Тогда уравнения движения жидкости, проинтегрированные по вертикали от
поверхности ![]() до дна
до дна ![]() , в
декартовой системе координат можно записать так:
, в
декартовой системе координат можно записать так:
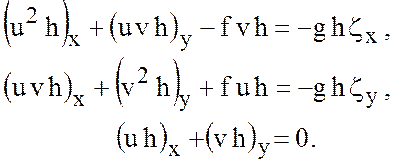 (7.28)
(7.28)
где первые два уравнения - это уравнения
движения, спроектированные на оси ![]() и
и ![]() соответственно, а третье – это уравнение
неразрывности. Здесь
соответственно, а третье – это уравнение
неразрывности. Здесь ![]() ,
, 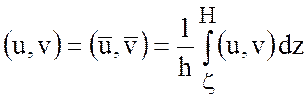 .
.
Запишем систему (7.28) в форме Громеки-Лэмба
![]() , (7.29)
, (7.29)
![]() , (7.30)
, (7.30)
где 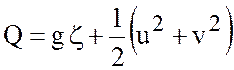 ,
, ![]() - абсолютный вихрь,
- абсолютный вихрь, ![]() - относительный вихрь. Далее, так как
изменения уровня
- относительный вихрь. Далее, так как
изменения уровня ![]() малы, то уравнение неразрывности перепишется в виде
малы, то уравнение неразрывности перепишется в виде ![]() . Значит, можно ввести функцию тока
. Значит, можно ввести функцию тока ![]() , удовлетворяющую равенствам
, удовлетворяющую равенствам ![]() и
и ![]() , тогда
, тогда 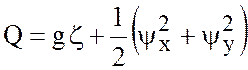 и
и ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.