Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 16

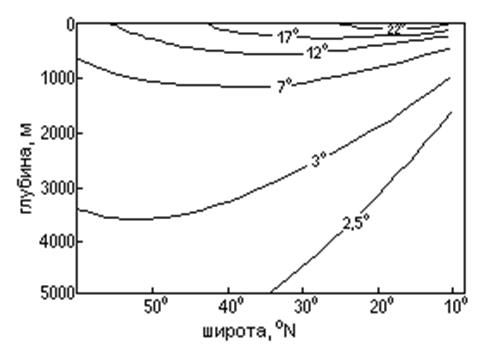
Рис. 7.11. Распределение температуры в модели Нидлера.

На риc. 7.11 показано меридиональное сечение поля температуры, рассчитанное Нидлером [14] по соотношениям (7.75) и

,                                         (7.81)

где выбрано

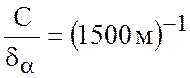
и поверхностная температура  пропорциональна . Такое распределение температуры по  удовлетворительно моделирует реальное распределение; изотермы поднимаются вблизи экватора (так как  пропорционально  и в северных широтах из-за уменьшения температуры на поверхности. Если  отрицательно, как это должно быть в крупномасштабном океанском круговороте, порожденном действием пассатных и западных ветров, то  также должно быть отрицательным, чтобы соответствующее бароклинное течение было направленно на юг.

Хотя соотношение (7.76) можно в принципе рассматривать как уравнение для , функция  и  должны иметь очень специальный вид, чтобы решение  этого уравнения было постоянным. Поэтому здесь мы задаем  и рассматриваем (7.76) как условие, налагаемое на ,  автомодельностью решения.

Отметим, что, согласно (7.78), вертикальная скорость на большой глубине   положительна; это одна из самых интересных особенностей построенного решения. При фиксированном  величина  полностью определяется параметром , характеризующим интенсивность диссипации. Если турбулентная диффузия плотности пренебрежимо мала (т.е.  близко к нулю), то  также обращается в нуль. Фактически здесь роль диссипации сводится лишь к созданию глубинного подъема вод. Действительно, (7.78) следует из уравнения

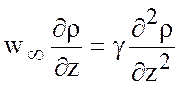,                                          (7.82)

в соответствии с которым вертикальная диффузия плотности балансируется подъемом глубинной холодной воды со скоростью . В то же время распределение плотности (7.75) является решением уравнений без диссипации, так как соответствующий потенциальный вихрь удовлетворяет соотношению

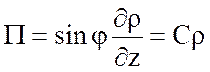.                                      (7.83)

Итак, динамика, описываемая рассмотренным простым автомодельным решением, расщепляется следующим образом. Основная структура полей в термоклине определяется сохранением потенциального вихря , в то время как диссипация определяет только величину скорости подъема глубинных вод, но не саму структуру термоклина. Возможно, в этом и заключается основная особенность автомодельной формы полученного решения.

Список литературы

1. Педлоски Дж. Геофизическая гидродинамика. 1984, М., Мир., 798 с.

2. Ле Блон П., Майзек Л. Волны в океане. 1981, т. 1, М., Мир, 365 с.

3. Каменкович В.М. Основы динамики океана. 1981, Л., Гидрометеоиздат,229 с.

4. Гилл А. Динамика атмосферы и океана. 1986, т.2, М., Мир, 415 с.

5. Озмидов Р. В.  Горизонтальная турбулентность и турбулентный обмен в океане. 1968, М.,  «Наука», 192 с.

6. Holland W.R. Oceanic General Circulation Models. In “The Sea”, Vol. 6, A Wiley-Interscience Publication, pp. 3-45.

7. Ekman V.W. On the influence of the Earth's rotation on ocean circulation. Arkiv. Mat. , Astr. och Phys., 1905, v. 2, No 11, 1-53

8. Шулейкин В.В. Физика моря. 1968, М., Наука., 1072 с.

9. Штокман В.Б. Уравнения поля полных потоков возбуждаемых ветром в неоднородном море. ЛАН СССР, 1946, т. 54, № 5, с. 407-410.

10. Саркисян А.С. Основы теории и расчет океанических течении. Л., Гидрометеоиздат, 1966, 122 с.

11. Stommel H. Westward intensification of wind-driven Ocean currents. Trans. Amer. Geophys. Union, 1948, v. 29, No 2, 202-206.

12. Fofonoff. N.P. Steady flow in a frictionless homogeneous ocean. J. Mar. Res., 1954, v. 13, No 3, 254-262.

13. Линейкин  П.С. Основные вопросы динамической теории бароклинного слоя моря. Л., Гидрометеоиздат, 1957, 139 с.

14. Needler G.T. A model for thermohaline circulation in an ocean of finite depth. J. Mar. Res.,1965, v. 23, No 3, 329-343.

15. Монин А.С.Геофизическая гидродинамика. 199?, М., «Наука», 300 с.