Анализ волновых движений в океане. Уравнения геофизической гидродинамики с учетом турбулентности. Пограничные слои в океане, страница 9

Из полученных уравнений следует, что в случае конечной глубины скорость поверхностного течения  может составлять с направлением ветра различные углы в зависимости от того, какова глубина моря по сравнению с глубиной трения. Действительно, тангенс угла между  и скоростью ветра (осью ) легко найти, разделив  на :

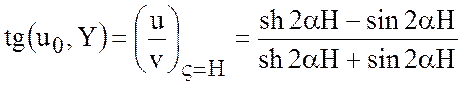.               (7.13)

Аргументом в этом выражении служит величина , которая зависит исключительно от отношения , следовательно, . При увеличении  угол сначала возрастает, доходит до некоторой максимальной величины около , а затем медленно уменьшается, стремясь к предельной величине . Дальнейшее увеличение глубины не отражается на исследуемом угле.

Расположение векторов скоростей течения, найденное по формулам (7.11), для случая конечной глубины, становится подобным расположению тех же векторов на рис. 7.8, когда глубина моря  превышает глубину трения , т.е. практически при таких глубинах моря его можно полагать бесконечно глубоким. Так, при  годограф векторов несущественно отличается от годографа рис. 7.8 в области, где скорости течения очень малы. Это обстоятельство важно для исследования дрейфовых течений.

Глубина трения в средних широтах и при средних скоростях ветра невелика (порядка 100 м). Следовательно, уравнения (7.11), как правило, можно применять в форме (7.6). Исключение составляет область Мирового океана в окрестности, где  стремится к нулю, а глубина трения в открытом море - к бесконечности.

На экваторе скорость установившегося дрейфового течения в самом поверхностном слое определяется на основании естественного условия: сила трения между воздухом и водой уравновешивается силами, действующими в поверхностном слое воды. Здесь нужно учитывать не только силу, выражаемую через коэффициент турбулентного внутреннего трения  и градиент соответствующей скорости течения по вертикали, но также и количество движения, отнимаемое у поверхностного слоя за счет вертикального потока масс, обусловленного турбулентностью.

Исследуем развитие дрейфового течения под действием ветра.

Пусть над морем, находившимся в состоянии полного покоя, возник ветер с некоторой определенной и постоянной скоростью. Примем этот момент за начало отсчета времени, тогда левые части уравнений (7.1) больше не обращаются в нуль, поскольку составляющие скорости  и  непрерывно возрастают, начиная с нуля.

По истечении некоторого промежутка времени ,  и  приобретут значения

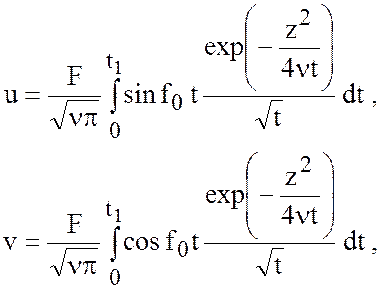                            (7.14)

                                               (7.15)

Пусть теперь промежуток времени, в течение которого работал ветер, выражается в новых единицах и равняется . Между величинами  и , измеренной в обычных единицах времени, существует соотношение

.

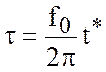С учетом (7.7), перепишем (7.4) в виде

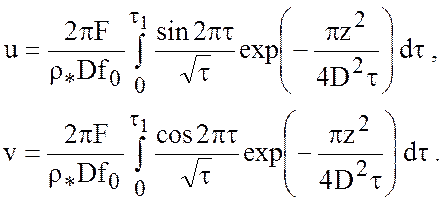                   (7.16)

В эти уравнения входит в качестве параметра величина . Следовательно, чем глубже лежит исследуемый слой, тем медленнее там будет устанавливаться движение, хотя абсолютные величины скоростей непрерывно уменьшаются с глубиной.

Конец вектора скорости описывает один оборот вокруг стационарного положения в течение 12 маятниковых часов. Можно считать поэтому, что поверхностная скорость, средняя за 24 маятниковых часа, равна по величине и направлению скорости установившегося течения на том же горизонте .

Соотношения между абсолютными величинами скоростей для различных глубоких горизонтов в случае неустановившегося течения тоже резко отличаются от тех же соотношений, вычисленных для установившегося течения. Так, при  течение через 24 часа достигает скорости, равной 1/7 скорости поверхностного течения; между тем в случае установившегося течения скорость эта составляла бы только .

7.2. Западный вязкий пограничный слой (теория Гольфстирима).

7.2.1. Метод полных потоков Штокмана.