Лекция №4
Введение в теорию переноса в газах.
Элементарное рассмотрение с кинетической точки зрения основных понятий теории газов является весьма грубым и по существу есть оценка порядков величин. Однако, с помощью такого рассмотрения удается выяснить основные качественные закономерности, и оно может быть полезными при анализе более сложных явлений, а введение поправочных коэффициентов позволяет в ряде случаев получать вполне удовлетворительные для практических целей количественные результаты.
С молекулярной точки
зрения давление газа на стенки сосуда есть результат передачи импульса
ударяющимися молекулами. Импульс, передаваемый единице поверхности в единицу
времени (давление) есть ![]() ~
~![]() , где
, где ![]() - поток;
- поток; ![]() -
средняя скорость;
-
средняя скорость; ![]() - объемная плотность частиц.
Откуда
- объемная плотность частиц.
Откуда
![]() ~
~![]() (4.1).
(4.1).
Определим температуру газа как меру средней кинетической энергии
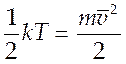 (4.2).
(4.2).
Тогда выражение (4.1) с учетом (4.2) примет вид
![]() (4.3),
(4.3),
известное как уравнение состояния идеального газа. Для частиц, описываемых Максвелловской функцией распределения, уравнение (4.3) может быть получено точно методами статистической физики.
Если имеется смесь N газов, находящихся при одной и той же температуре то
![]() ~
~ 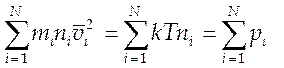 (4.4),
(4.4),
где ![]() -
парциальное давление. Формула (4.4) выражает закон Дальтона.
-
парциальное давление. Формула (4.4) выражает закон Дальтона.
Тепловое движение частиц приводит к постоянному их перемешиванию и обмену импульсом и энергией в процессе столкновений между собой. В результате в газе происходит выравнивание имеющихся неоднородностей и дает начало нескольким процессам, в зависимости от характера этих неоднородностей:
1. диффузии – при наличии неоднородности концентрации частиц различного сорта;
2. теплопроводности – если изначально имелась область неоднородно нагретого газа;
3. вязкого трения – если имелась скоростная неоднородность.
Все эти явления являются необратимыми процессами и имеют много общего: происходит перенос некой величины (массы, энергии или количества движения) из одной части вещества в другую и могут быть рассмотрены единообразно. Прежде чем перейти к непосредственному рассмотрению процессов переноса необходимо определить важные с точки зрения столкновительных процессов средние характеристики: частоту столкновений и длину свободного пробега.
Частота столкновений и средняя длина свободного пробега.
Движение двух тел в пространстве (рис. 4.1) может быть
представлено 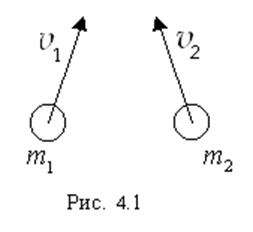 в виде их относительного
движения со скоростью
в виде их относительного
движения со скоростью ![]() , массой
, массой 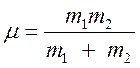 и движения их центра масс со скоростью
и движения их центра масс со скоростью
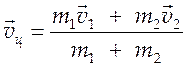 с суммарной массой
с суммарной массой ![]() . Определим функции вероятностей
распределения частиц по скоростям для каждого из этих движений. Запишем
вероятность сложного события: первая частица имеет скорость
. Определим функции вероятностей
распределения частиц по скоростям для каждого из этих движений. Запишем
вероятность сложного события: первая частица имеет скорость![]() , а вторая скорость
, а вторая скорость ![]() :
:![]() (т.к. эти события статически независимы). Для
простоты, будем считать, что
(т.к. эти события статически независимы). Для
простоты, будем считать, что ![]() и
и ![]() есть
Максвелловские сферически симметричные функции распределения вероятностей, тогда
есть
Максвелловские сферически симметричные функции распределения вероятностей, тогда
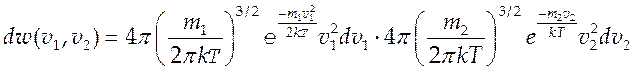 (4.5).
(4.5).
Перейдем в (4.5) от ![]() и
и ![]() к
к ![]() и
и![]() по
формулам
по
формулам
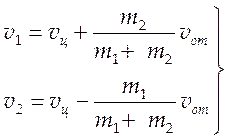 (4.6).
(4.6).
Для кинетической энергии системы имеем:
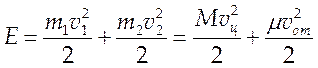 (4.7).
(4.7).
С учетом (4.6) и (4.7) выражение (4.5) в новых переменных запишется:
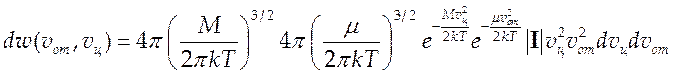 (4.8),
(4.8),
где якобиан преобразования:
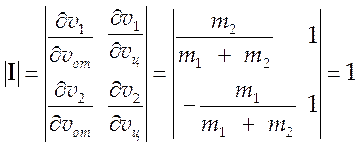 .
.
Поскольку ![]() , то из (4.8) следует выражение для функции
распределения по относительным скоростям
, то из (4.8) следует выражение для функции
распределения по относительным скоростям
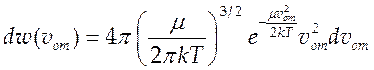 (4.9).
(4.9).
C учетом распределения (4.9) средняя скорость относительного движения есть:
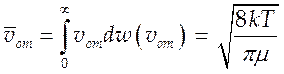 (4.10).
(4.10).
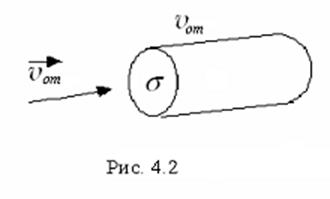 Найдем среднюю частоту столкновений молекул в газе.
Если одну из молекул взять в качестве пробной, то она столкнется со всеми
другими молекулами, находящимися в цилиндре объемом
Найдем среднюю частоту столкновений молекул в газе.
Если одну из молекул взять в качестве пробной, то она столкнется со всеми
другими молекулами, находящимися в цилиндре объемом ![]() и
обладающими заданной скоростью относительно движения
и
обладающими заданной скоростью относительно движения ![]() , (рис. 4.2)
число которых есть
, (рис. 4.2)
число которых есть ![]() . Тогда число
столкновений можно определить как
. Тогда число
столкновений можно определить как
![]() (4.11).
(4.11).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.