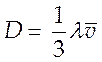Введение в теорию переноса в газах, страница 3

                                                                                                 (4.28).

Теплопроводность

Пусть  - количество тепла переносимое в процессе теплопроводности. Чтобы рассмотреть этот процесс в чистом виде мы должны исключить диффузионные потоки и работу газа, т.е. положить n = const, (тогда при постоянном числе частиц N следует V = constи ). В этом случае , где  - теплоемкость на одну молекулу и из (4.8) получим

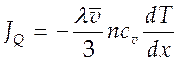                                                                                      (4.29).

Для процесса теплопроводности известен экспериментальный закон Фурье

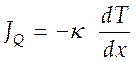                                                                                            (4.30),

где  - коэффициент теплопроводности. Сравнивая (4.13) и (4.14) находим теоретическое выражение для коэффициента теплопроводности

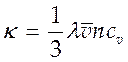                                                                                             (4.31).

Вязкое трение

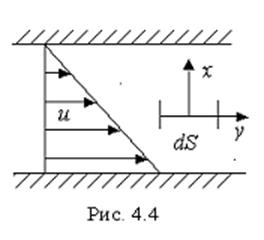Вязкое трение наблюдается в случае наличия скоростной неравновесности газового потока. Рассмотрим перенос количества движения за время  через площадку , расположенную параллельно скорости газовых слоев (рис. 4.4) и нормальную градиенту скорости. Для исключения эффектов диффузии и теплопроводности будем считать  = соnst и  = соnst. В рассматриваемом случае  - переносимый импульс, а  - импульс одной молекулы. Из (4.21) и (4.24) имеем:

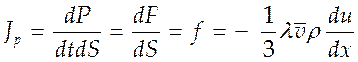          (4.32).

Здесь мы использовали, что , а  - сила трения, действующая на единичную площадку и направленная по касательной к поверхности площадки. Для вязкого трения известен экспериментальный закон (закон Ньютона):

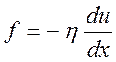                                                                                               (4.33).

Из сопоставления (4.32) и (4.33) следует выражение для коэффициента вязкого трения

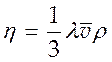                                                                                               (4.34).

Не трудно видеть, что в рамках представленной элементарной теории отношение коэффициента теплопроводности к коэффициенту вязкого трения есть 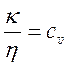 и легко может быть проверено экспериментально. Эксперимент подтверждает это соотношение, но с неким поправочным множителем, т.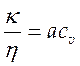е. , где .

Таким образом, в рамках элементарной кинетической теории коэффициенты переноса однозначно определяются, если каким либо образом получены соответствующие эффективные сечения столкновений. Этот же результат остается верен и при более строгом подходе к рассмотрению явлений переноса.

Плотность электрического тока и проводимость

В плазме при наличие внешнего электрического поля начинает течь ток, плотность которого есть

                                                                                                   (4.35),

где средняя скорость электронов в направлении поля. На каждый электрон действует сила , придающая электрону ускорение . За время между двумя ближайшими столкновениями электрон наберет скорость 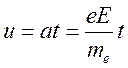 . Полагая , где средняя частота столкновений, получим 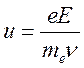. Средняя скорость есть  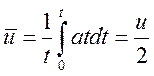и для плотности тока будем иметь

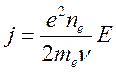                                                                                                         (4.36).

Известен экспериментальный закон Ома для тока проводимости

                                                                                                              (4.37).

Из сравнения (4.36) и (4.37) следует выражение для проводимости

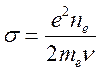                                                                                                           (4.38).

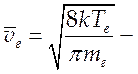Рассмотрим полностью ионизованную плазму. Из (4.13) с учетом, что масса электрона много меньше массы иона и эффективное сечение электрон-электронных столкновений  много меньше электрон-ионных  имеем , где средняя скорость теплового движения. Как будет показано ниже, 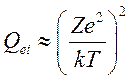и для проводимости получаем выражение

                                                                                                           (4.39),

известное как закон Спитцера.

Выпишем отношение коэффициента электронной теплопроводности (4.31) к проводимости (4.38) 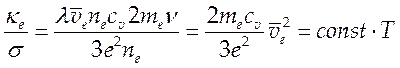, откуда для полностью ионизованной плазмы следует

                                                                                                   (4.40)

закон Видемана-Франца.