Полное число столкновений находится интегрированием (4.11) по всем скоростям относительно движения:
v = 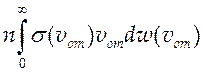 (4.12).
(4.12).
Вводя некоторое среднее сечение
столкновений ![]() и вынося его из под знака интеграла в (4.12), получим
и вынося его из под знака интеграла в (4.12), получим
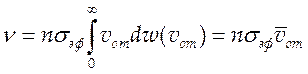 (4.13).
(4.13).
Для частиц с одинаковой массой ![]() (приведенная масса
(приведенная масса 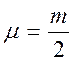 )
частота столкновений запишется
)
частота столкновений запишется
![]() ;
; ![]() (4.14).
(4.14).
Среднее время между двумя столкновениями есть
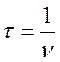 (4.15).
(4.15).
Определим среднюю длину свободного пробега как:
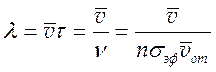 (4.16).
(4.16).
Для Максвелловских частиц 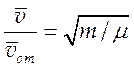 и из (4.16) следует выражение для длины
свободного пробега
и из (4.16) следует выражение для длины
свободного пробега
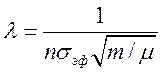 (4.17).
(4.17).
Для газа, состоящего из частиц одного
сорта, 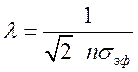 и зависит только от плотности n. Для смеси частиц различного сорта,
длина пробега частиц сорта i
есть:
и зависит только от плотности n. Для смеси частиц различного сорта,
длина пробега частиц сорта i
есть:
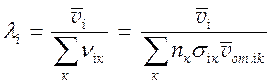 (4.18),
(4.18),
где 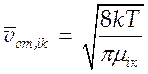 ,
, 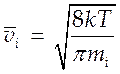 ,
, ![]() , а
, а ![]() - эффективные или газокинетические радиусы
частиц. Тогда
- эффективные или газокинетические радиусы
частиц. Тогда
![]()
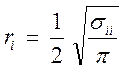 ;
; 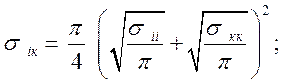
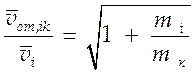 и выражение (4.18) преобразуется к виду:
и выражение (4.18) преобразуется к виду:
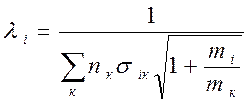 ,
, ![]() …. (4.19).
…. (4.19).
Для газа, состоящего из смеси частиц двух сортов из (4.19) получим:
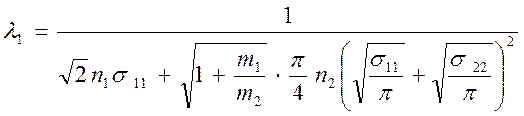
(4.20).
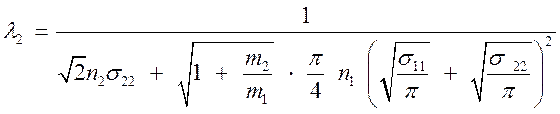
Элементарная кинетическая теория переноса.
Рассмотрим область,
занятую газом и выберем внутри некую площадку ![]() , через
которую переносится физическая величина «В». Для простоты бу
, через
которую переносится физическая величина «В». Для простоты бу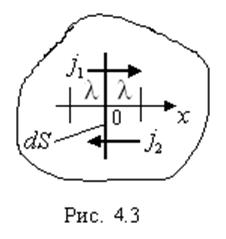 дем считать, что перенос идет только
в одном направлении
дем считать, что перенос идет только
в одном направлении ![]() , нормальном к выбранной площадке
, нормальном к выбранной площадке
![]() (рис. 4.3). Запишем полный поток
(рис. 4.3). Запишем полный поток ![]() величины В через площадку, равный
разности односторонних потоков. По определению
величины В через площадку, равный
разности односторонних потоков. По определению
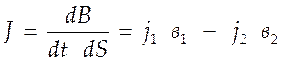 (4.21),
(4.21),
где ![]() -
односторонний поток частиц,
-
односторонний поток частиц, ![]() - значение величины
- значение величины ![]() на одну частицу. При подсчете потока
на одну частицу. При подсчете потока ![]() будем считать, что в каждом из трех
взаимно перпендикулярных направлений переносится одинаковое число частиц – 1/3
от общего числа. Тогда в положительном направлении
будем считать, что в каждом из трех
взаимно перпендикулярных направлений переносится одинаковое число частиц – 1/3
от общего числа. Тогда в положительном направлении ![]() будет
переносится 1/6 всех частиц (т.н. шестигрупповое приближение). В этом случае
будет
переносится 1/6 всех частиц (т.н. шестигрупповое приближение). В этом случае 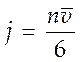 , где
, где ![]() - число
частиц в единице объема, а
- число
частиц в единице объема, а ![]() - средняя скорость и
уравнение (4.21) запишется:
- средняя скорость и
уравнение (4.21) запишется:
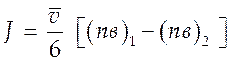 (4.22).
(4.22).
Очевидно, что частицы,
проходящие через сечение ![]() , переносят неизменную
информацию только из слоев газа, отстоящих от этого сечения на расстоянии
средней длины свободного пробега
, переносят неизменную
информацию только из слоев газа, отстоящих от этого сечения на расстоянии
средней длины свободного пробега ![]() и
и ![]() ;
; ![]() , а
(4.22) перепишется
, а
(4.22) перепишется
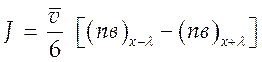 (4.23).
(4.23).
Проводя разложение в правой части
(4.23) по малой величине ![]() , получим
, получим
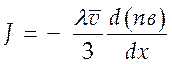 (4.24),
(4.24),
где знак минус означает, что перенос идет в направлении противоположном градиенту.
Рассмотрим в начале
простейший случай, когда происходит диффузия молекул некоторого газа в среде
молекул того же газа, т.н. самодиффузию. При этом мы должны предположить, что
суммарная концентрация частиц в единице объема постоянна, иначе при ![]() - соnst из уравнения состояния следовало бы наличие градиента
давления, что привело бы к течению газа. Поэтому следует рассмотреть такой газ,
где
- соnst из уравнения состояния следовало бы наличие градиента
давления, что привело бы к течению газа. Поэтому следует рассмотреть такой газ,
где ![]() - соnst, а в общей массе газа есть молекулы каким либо
образом помеченные (например, радиоактивные изотопы) и эти молекулы диффундируют
в остальном газе. Пусть концентрация меченых молекул
- соnst, а в общей массе газа есть молекулы каким либо
образом помеченные (например, радиоактивные изотопы) и эти молекулы диффундируют
в остальном газе. Пусть концентрация меченых молекул ![]() ,
а остальных
,
а остальных ![]() , тогда
, тогда ![]() ;
; ![]() .
.
В данном случае
переносимой величиной В есть масса меченного газа: ![]() ,
, ![]() ;
; ![]() - плотность меченного газа и из (4.8)
следует для потока массы
- плотность меченного газа и из (4.8)
следует для потока массы
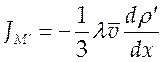 (4.25).
(4.25).
Разделив (4.25) на ![]() , получим выражение для потока частиц через
концентрацию
, получим выражение для потока частиц через
концентрацию ![]()
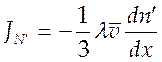 (4.26).
(4.26).
Для процесса диффузии известен экспериментальный закон Фика
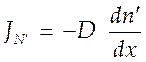 (4.27),
(4.27),
где D - коэффициент самодиффузии. Сравнивая (4.26) и (4.27) находим, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.