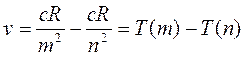Лабораторный практикум по оптике, содержащий описание 21 лабораторной работы, страница 53

,                     (17.11)

Отсюда следует вывод, что частоты всех линий в спектре водорода могут быть представлены в виде разности двух функций от целых чисел и. Эти функции носят название спектральных термов.

Теория спектра водорода базируется на трех постулатах Бора:

1. Электрон в атоме водорода может находиться лишь на орбитах строго определенного радиуса, называемых стационарными. На этих орбитах момент количества движения электрона mV_kr_k кратен целому числу , т.е.

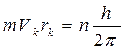                                (17.12)

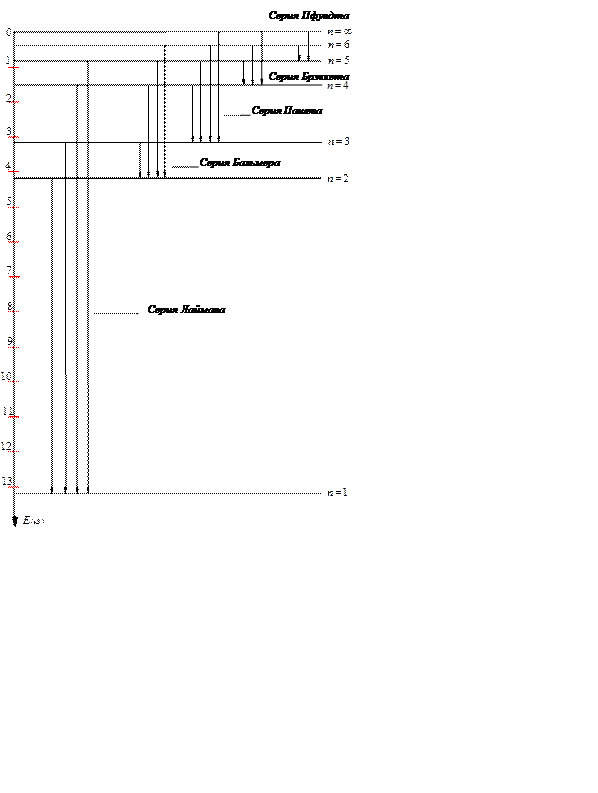
Рис. 17.1.

где m = 9,1´10^–31 кг  – масса электрона,

      V_k – скорость электрона на k-той орбите,

      r_k – радиус k-той орбиты,

      h = 6,62´10^-34 Дж´с – постоянная Планка,

      n – квантовое число, n = 1,2,3,4...

2. Движение электрона по стационарным орбитам не сопровождается излучением или поглощением энергии.

3. При переходе электрона с одной стационарной орбиты на другую излучается или поглощается квант энергии, частота которого определяется условием Бора:

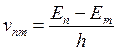,                                  (17.13)

где Е_n и Е_m – соответственно энергия электрона на n-той и m-той орбитах.

Согласно теории полная энергия электрона в атоме отрицательна и равна

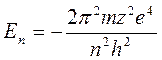,                              (17.14)

где m и e – масса и заряд электрона (е = 1,6´10^-19 Кл);

      z – порядковый номер элемента в таблице Менделеева;

      n – номер орбиты, на которой находится электрон.

Введем обозначения:

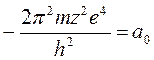,                               (17.15)

Тогда (17.14) перепишется в виде:

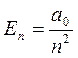                                      (17.16)

Подставим (17.16) в (17.13)  и получим:

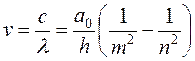.                         (17.17)

Отсюда

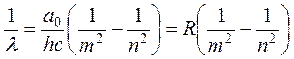,                 (17.18)

то есть мы получили формулу, совпадающую с выражением (17.10).

Величину

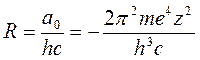                           (17.19)

называют постоянной Ридберга. С помощью формулы (17.18), измерив на опыте длины волн видимой части спектра водорода, можно вычислить постоянную Ридберга R.

ОПИСАНИЕ УСТАНОВКИ

Для определения наибольшей длины волны в спектре поглощения водного раствора (K₂Cr₂O₇) используют монохроматор УМ-2. Монохроматор (рис. 17.2) размещают на двух оптических рельсах 1.

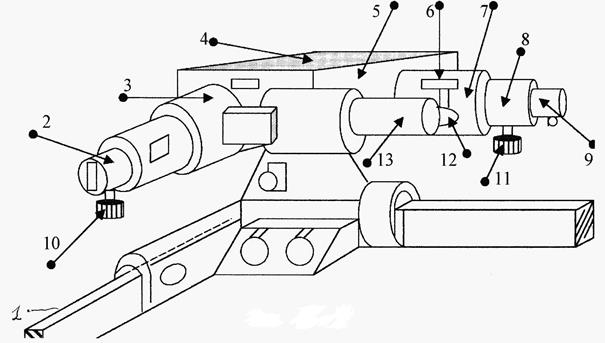
Рис. 17.2.

Он состоит из входной трубы 3 со щелью 2, призменного столика 5 с призмой 4, находящихся внутри корпуса, выходной коллимационной трубы 8 и щели 9. Ширина раскрытия щелей регулируется маховичками 10. Поворот призмы осуществляется барабаном 13. Фокусировка выходной трубы производится маховичками 12.

Положение коллиматора выходной трубы определяется по миллиметровой шкале с нониусом 6. В трубе коллиматора между щелью и окуляром помещен затвор, с помощью которого можно прекратить доступ света в прибор. Управление затвором осуществляется с помощью рукоятки 11.

Оптическая схема монохроматора приведена на рис. 17.3.

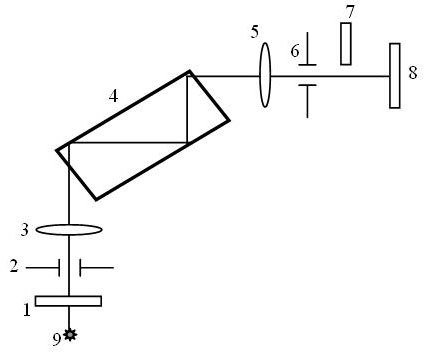
Рис. 17.3.

Луч света от источника 9 через щель 2 и объектив 3 попадает на диспергирующую призму 4 и разлагается в спектр. Призма поворачивает лучи на 90°. На пути пучка света помещается выходная труба монохроматора, состоящая из окуляра 5 и щели 6. Щели закрываются защитными стеклами 1 и 8.

Включение в сеть ртутной лампы и лампы сплошного спектра осуществляется через блок питания.

ВЫПОЛНЕНИЕ РАБОТЫ

Устанавливают ртутную лампу на оптический рельс на расстоянии 453 мм от входной щели прибора. Между входной щелью и ртутной лампой помещают ахроматический конденсор с f = 94 мм на расстоянии 130 мм от входной щели. На входную щель надевают насадку с линзой с фокусным расстоянием f = 140 мм. Вращением барабана 10 устанавливают ширину входной щели 0,01 – 0,02 мм. Подсоединяют ртутную лампу к блоку питания, включают тумблер питания.

УПРАЖНЕНИЕ I

Градуирование шкалы монохроматора

1.  Нажатием кнопки включают ртутную лампу.

2.  Направляют свет лампы на щель монохроматора. Перемещением линзы по оптическому рельсу фокусируют излучение лампы на щель прибора.