Цель работы: Определить постоянные Планка и Ридберга экспериментальным путем.
Приборы и принадлежности: монохроматор УМ-2, ртутная лампа с источником питания, водородная трубка с узлом крепления, высоковольтный индуктор, источник питания на 12 В, раствор двухромовокислого калия, подъемный столик.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Нагретое до определенной температуры тело становится источником излучения электромагнитных волн различной длины, в том числе и оптического диапазона. В спектрах твердых тел и жидкостей существуют волны практически всех длин. Эти спектры называют сплошными. Спектры паров газов представляют собой набор широких окрашенных полос, разделенных темными промежутками, или отдельные линии, разделенные темными промежутками. Такие спектры называют полосатыми или линейчатыми. Все эти спектры обусловлены испусканием электромагнитных волн и объединены общим названием эмиссионных или атомных спектров.
Если на окрашенный раствор направить излучение от источника сплошного спектра, то на его фоне образуются отдельные темные линии. Такой спектр связан с поглощением веществом отдельных электромагнитных волн и его называют абсорбционным спектром или спектром поглощения.
Спектр поглощения используется для определения постоянной Планка. Направим на кювету с раствором двухромовокислого калия (K2Cr2O7) световой поток. Прохождение света через раствор сопровождается его поглощением. Поглощение света приводит к распаду молекулы двухромовокислого калия на ионы. Распад происходит по схеме:
K2Cr2O7→K2+++Cr2O7 – – (17.1)
Экспериментально
найдено, что распад происходит, если молекуле сообщается энергия не менее 3,97´10–19Дж. Следовательно,
минимальная энергия фотонов, поглощаемых раствором,
hv = 3,97·10–19Дж.
Отсюда
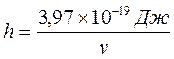 , (17.2)
, (17.2)
где v – минимальная частота.
Учитывая связь
частоты с длиной волны (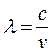 ), имеем:
), имеем:
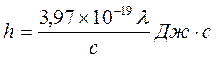 , (17.3)
, (17.3)
где с – скорость света; λ – наибольшая длина волны в спектре поглощения раствора (K2Cr2O7), определенная с помощью монохроматора.
Наиболее простым атомным спектром является спектр легчайшего химического элемента –– водорода.
В 1885 году швейцарский физик Бальмер, изучая видимую часть этого спектра, экспериментальным путем установил наличие определенной закономерности, связывающей между собой длины волн отдельных спектральных линий. Им установлена формула:
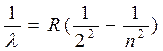 , (17.4)
, (17.4)
где n = 3,4,5..., R = 1,097 ´ 10–7 м–1 – постоянная Ридберга.
Величину
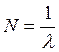 (17.5)
(17.5)
называют волновым числом. Оно показывает, сколько длин волн укладывается в 1м.
Линии в спектре водорода, описываемые формулой (17.4), составляют спектральную серию Бальмера. В видимой области спектра лежат только четыре линии этой серии. В настоящее время обнаружено 29 линий серии Бальмера, 25 из которых лежат в близкой ультрафиолетовой части спектра.
В 1906 году Лайман открыл в далекой ультрафиолетовой области спектра водорода серию линий, описываемых формулой:
![]() (17.6)
(17.6)
где n = 2,3,4... .
В 1908 году серию линий в близкой инфракрасной области водородного спектра обнаружил Пашен. Она описывается формулой
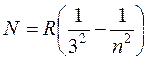 (17.7)
(17.7)
где n = 4,5,6... .
И, наконец, Брэккет (1922г.) и Пфундт (1930г.) нашли еще две серии линий в более далеких областях инфракрасной части спектра водорода. Формулы, описывающие эти серии, имеют вид:
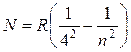 , где n =
5,6,7… (17.8)
, где n =
5,6,7… (17.8)
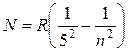 , где n =
6,7… (17.9)
, где n =
6,7… (17.9)
Если объединить соотношения (17.4), (17.6) – (17.9), то получим универсальную формулу
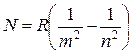 ,
(17.10)
,
(17.10)
где число m принимает целые значения m = 1,2,3... и определяет серию, число n удовлетворяет неравенству n > m и определяет отдельные линии серии. Эти серии приведены на рис. 17.1.
Подставив
соотношение (17.5) в (17.10) и учитывая, что 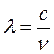 ,
получим:
,
получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.