Лабораторный практикум по оптике, содержащий описание 21 лабораторной работы, страница 23

№ п/п
1
2
3
4
5

3.  По данным таблицы 2 построить графики зависимости:

       и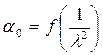       

Сделать выводы.

4.  Определить углы вращения плоскости поляризации для 4-х растворов сахара с концентрациями , , ,  для длины волны  (светофильтр ОС-11) и одного-двух растворов с неизвестной концентрацией . Результаты занести в таблицу 3.

Таблица3. Зависимост угла вращения плоскости поляризации от концентрации раствора сахара С.

№ п./п	Концентрация
									Для раствора неизвестной концентрации
1
2
3
4
5

Результат:

5.  Построить график зависимости  и с помощью графика определить неизвестную концентрацию  раствора сахара.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.  Сущность явления поляризации света.

2.  Какой свет называется плоско поляризованным?

3.  Какой свет называется циркулярно поляризованным?

4.  Получение и анализ поляризованного света.

5.  Поляризационные приборы. Принцип их работы.

6.  Что такое вращение плоскости поляризации света? Оптически активные вещества.

7.  Принцип работы поляриметров.

ЛАБОРАТОРНАЯ РАБОТА №7

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ПРИ ПОМОЩИ БИПРИЗМЫ ФРЕНЕЛЯ

Цель работы: определить длину световой волны интерференционным методом.

Приборы и принадлежности: бипризма, микроскоп, оптическая скамья, фонарь, светофильтр, линза, матовый экран, линейка.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ

Два источника света называются когерентными, если разность фаз между испускаемыми волнами остаётся постоянной, и эти волны имеют одинаковую частоту.

Пусть имеем два когерентных источника света S₁ и S₂, расположенных на расстоянии l между собой (рис. 8.1).

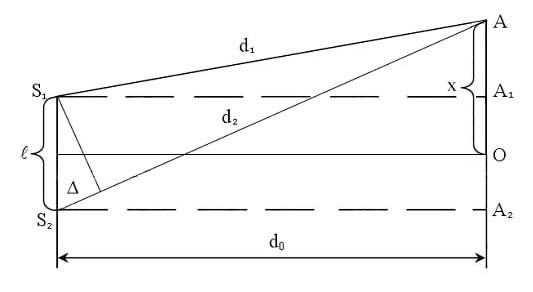
Рис. 8.1.

Рассмотрим интерференционную картину на экране Э, отстоящем на расстоянии d₀ от линии S₁S₂, в точке А. Обозначим расстояние от точек S₁ и S₂ до точки А через d₁ и d₂, и расстояние ОА через x. Характер интерференционной картины в точке А определяется оптической разностью хода лучей D=d₁-d₂. Найдём D. Из треугольников S₁AA₁ и S₂AA₂ имеем:

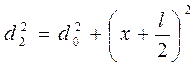                            (8.1)

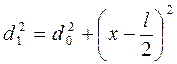,                             (8.2)

где A₁O=OA₂=.

Вычитая из (8.1) (8.2), имеем:

                                   (8.3)

С другой стороны, т.к. d₀ >> l, то

         (8.4)

Приравняв (8.3) и (8.4), получим:

,

отсюда

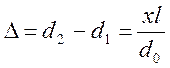                               (8.5)

В точке А будет наблюдаться максимум, если

D=ml, (m=0,1,2,3,4…)                             (8.6)

и минимум, если

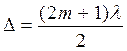                                    (8.7)

Тогда расстояние до m-ой светлой полосы равно: 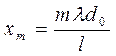, а до m+1 полосы: .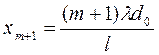

Вычитая из второго равенства первое, получим ширину интерференционной полосы:

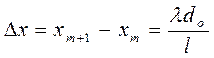
                       (8.8)

Отсюда длина световой волны равна

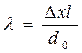 .                                       (8.9)